Danh mục
ToggleTrong số các môn thi vào lớp 10 bắt buộc, môn Toán luôn là nỗi lo của nhiều bạn bởi nội dung kiến thức trải dài, đòi hỏi tư duy logic và khả năng vận dụng cao. Tuy nhiên, nếu biết cách ôn tập đúng hướng, các em hoàn toàn có thể làm chủ môn học này. Một trong những chìa khóa thành công chính là nắm vững kiến thức trọng tâm thi vào 10 môn Toán.
Hiểu được điều đó, bài viết này sẽ giúp các em hệ thống lại toàn bộ các kiến thức trọng tâm thi vào 10 môn Toán, từ đại số đến hình học, từ các dạng bài cơ bản đến các dạng nâng cao thường gặp trong đề thi. Với định hướng rõ ràng và phương pháp học phù hợp, việc đạt điểm cao môn Toán không còn là điều quá khó khăn.
Những kiến thức ôn thi Toán vào 10 trọng tâm cần ghi nhớ

Tải Mindmap đầy đủ về Kiến thức trọng tâm thi vào 10 môn Toán tại Link GG Drive
1. Căn thức đại số
Căn thức đại số là nền tảng quan trọng trong chương trình Toán THCS và thường xuyên xuất hiện trong đề thi vào lớp 10. Việc nắm vững cách rút gọn, quy đồng và thực hiện phép toán với căn thức giúp học sinh xử lý nhanh các bài toán về biểu thức và phương trình.

Ví dụ bài tập:





Những bài toán về căn thức đại số thường rất đa dạng, từ cơ bản đến nâng cao. Việc luyện tập thường xuyên với các ví dụ trên sẽ giúp học sinh:
- Nắm chắc quy tắc biến đổi.
- Giải nhanh bài tập trong đề thi vào 10.
- Hạn chế sai sót trong tính toán.
Dạng bài thường gặp trong đề thi – Căn thức đại số
Trong đề thi tuyển sinh vào lớp 10 môn Toán, phần căn thức đại số thường được khai thác qua các dạng bài cơ bản đến nâng cao. Mục tiêu của các dạng bài này không chỉ kiểm tra kỹ năng tính toán mà còn là khả năng biến đổi biểu thức linh hoạt, chính xác. Dưới đây là những dạng bài tiêu biểu học sinh cần chú trọng ôn luyện.
Dạng 1: Rút gọn biểu thức chứa căn
Yêu cầu học sinh vận dụng các công thức căn thức để rút gọn về dạng đơn giản nhất.
Công thức thường dùng:

Ví dụ:

Dạng 2: Trục căn thức ở mẫu
Biến đổi để mẫu số của phân thức không còn chứa căn bậc hai.
Công thức thường dùng:

Ví dụ:

Dạng 3: Tìm điều kiện để biểu thức có nghĩa
Biểu thức chứa căn thức chỉ có nghĩa khi biểu thức trong căn không âm.
Công thức áp dụng:

Ví dụ:

Dạng 4: So sánh hai biểu thức căn thức
Đưa hai biểu thức về cùng dạng, hoặc sử dụng bình phương để so sánh.
Ví dụ:

Phần căn thức đại số trong đề thi vào 10 tuy không quá khó nhưng thường được lồng ghép vào các bài toán tổng hợp. Học sinh cần luyện thành thạo các dạng bài cơ bản như rút gọn, trục căn thức, tìm điều kiện xác định… để tự tin xử lý mọi bài toán dạng này. Đừng quên luôn kiểm tra điều kiện có nghĩa trước khi tính toán để tránh mất điểm không đáng có.
2. Hàm số
Trong hệ thống kiến thức trọng tâm thi vào 10 môn Toán, hàm số bậc nhất là nội dung then chốt của chương trình lớp 9. Đây là phần không chỉ kiểm tra khả năng tính toán mà còn đánh giá tư duy phân tích và vận dụng của học sinh thông qua việc vẽ đồ thị, xác định mối quan hệ giữa các đại lượng, và giải các bài toán thực tế. Nắm chắc phần này giúp học sinh dễ dàng ghi điểm ở câu đầu tiên của đề thi – nơi thường đặt các câu hỏi cơ bản và dễ ăn điểm.
Hàm số bậc nhất
Dạng tổng quát:
𝑦 = 𝑎𝑥 + 𝑏(𝑎≠0)
Trong đó:
- 𝑎: hệ số góc, quyết định độ nghiêng của đường thẳng.
- 𝑏: tung độ gốc, là điểm mà đường thẳng cắt trục tung.
Tính chất của hàm số bậc nhất
- Đồng biến: nếu 𝑎 > 0, khi 𝑥 tăng thì 𝑦 cũng tăng.
- Nghịch biến: nếu 𝑎 < 0, khi 𝑥 tăng thì 𝑦 giảm.
- Đồ thị của hàm số bậc nhất là đường thẳng.
Cách vẽ đồ thị hàm số bậc nhất
- Chọn 2 giá trị bất kỳ của 𝑥, tính 𝑦 tương ứng để xác định 2 điểm.
- Nối 2 điểm lại ta được đường thẳng biểu diễn đồ thị.
Xác định điểm cắt trục
Cắt trục tung tại điểm có hoành độ bằng 0:
𝑥 = 0 ⇒ 𝑦 = 𝑏 ⇒ 𝐴(0;𝑏)
Cắt trục hoành tại điểm có tung độ bằng 0:

Ví dụ 1: Vẽ đồ thị hàm số
Đề bài:
Vẽ đồ thị hàm số
𝑦 = 2𝑥 − 1
Giải:
- Chọn 𝑥 = 0 → 𝑦 = −1 ⇒ 𝐴(0;−1)
- Chọn 𝑥 = 1 → 𝑦 = 1 ⇒ 𝐵(1;1)
- Nối hai điểm A và B ta được đường thẳng là đồ thị hàm số𝑦 = 2𝑥 − 1
Nhận xét:
- 𝑎 = 2 > 0 → hàm số đồng biến
- Cắt trục tung tại (0;−1), trục hoành tại

Hàm số bậc nhất là phần kiến thức dễ hiểu nhưng không kém phần quan trọng trong hệ thống kiến thức trọng tâm thi vào 10 môn Toán. Việc nắm chắc bản chất hàm số, thành thạo cách vẽ đồ thị và giải các bài toán ứng dụng không chỉ giúp học sinh làm tốt phần đại số mà còn tạo nền tảng vững chắc cho những nội dung hình học và vận dụng sau này.
3. Vị trí tương đối của hai đường thẳng
Một nội dung quen thuộc nhưng thường bị học sinh xem nhẹ trong quá trình ôn tập đó là vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ. Việc hiểu và vận dụng tốt phần này là một lợi thế giúp học sinh nhanh chóng ăn điểm trong đề thi. Vì thế, đây là một phần kiến thức trọng tâm thi vào 10 môn Toán không thể bỏ qua.

Ví dụ: Nhận biết vị trí hai đường thẳng
Cho hai hàm số:
𝑦 = 2𝑥 + 1 và 𝑦 = 2𝑥 − 3
Xác định vị trí tương đối của hai đường thẳng.
Giải: Ta thấy
𝑎1 = 𝑎2 nhưng 𝑏1 ≠ 𝑏2 → Hai đường song song.
Kết luận: Hai đường thẳng không cắt nhau trong mặt phẳng tọa độ.
Việc phân tích vị trí tương đối của hai đường thẳng là phần dễ ăn điểm nhưng lại có tính ứng dụng cao trong các bài toán liên quan đến hàm số và hệ phương trình. Đây chính là mảnh ghép quan trọng trong kiến thức trọng tâm thi vào 10 môn Toán, giúp học sinh vừa làm tốt các câu hỏi cơ bản, vừa chuẩn bị nền tảng cho các bài toán vận dụng thực tế.
4. Phương trình bậc hai
Trong các đề thi tuyển sinh vào lớp 10, phương trình bậc hai luôn là phần xuất hiện với tần suất cao trong các câu hỏi về đại số. Đây là kiến thức trọng tâm của chương trình lớp 9, thường được lồng ghép với các dạng bài như giải phương trình, biện luận số nghiệm, bài toán có lời văn, bài toán thực tế…
Vì vậy, phương trình bậc hai là một phần không thể thiếu trong hệ thống kiến thức trọng tâm thi vào 10 môn Toán mà học sinh cần nắm vững.
Dạng tổng quát của phương trình bậc hai một ẩn:
ax² + bx + c = 0 (a≠0)
Công thức tính biệt thức (delta):
Δ = b² – 4ac
Công thức nghiệm:
- Nếu Δ > 0: phương trình có hai nghiệm phân biệt

- Nếu Δ = 0: phương trình có nghiệm kép

- Nếu Δ<0: phương trình vô nghiệm
Ví dụ: Giải phương trình bậc hai cơ bản
𝑥² − 5x + 6 = 0

Phương trình bậc hai không chỉ là phần bài tập quen thuộc trong các đề thi mà còn là nền tảng để giải các bài toán có lời văn, bài toán thực tế – những câu hỏi thường chiếm nhiều điểm. Việc thành thạo giải phương trình bậc hai giúp học sinh xây dựng sự tự tin và nâng cao năng lực giải toán tổng hợp – đúng với mục tiêu rèn luyện kiến thức trọng tâm thi vào 10 môn Toán.
5. Hệ thức lượng trong tam giác vuông
Đây là một phần kiến thức trọng tâm thi vào 10 môn Toán mà bất kỳ học sinh nào cũng cần nắm vững nếu muốn đạt điểm tối đa ở phần hình học. Hệ thức lượng trong tam giác vuông giúp học sinh giải nhanh các bài toán liên quan đến độ dài cạnh, đường cao, trung tuyến trong tam giác vuông.

Cho tam giác vuông ABC tại A, đường cao AH hạ từ đỉnh vuông góc với cạnh huyền BC. Gọi AB=c, AC=b, BC=a, AH=h, BH=x, CH=y.
Hệ thức giữa cạnh góc vuông và hình chiếu trên cạnh huyền:
- AB² = BH . BC (c² = a⋅x)
- AC² = CH . BC (b² = a⋅y)
Hệ thức giữa đường cao và hình chiếu:
AH² = AH . CH (h² = x . y)
Hệ thức giữa cạnh huyền và đường cao ứng với cạnh huyền:
AB . AC = AH . BC (bc = ah)
Ví dụ: Tính độ dài đường cao
Cho tam giác vuông ABC vuông tại A, BC=13, AB=5, AC=12. Tính đường cao AH từ A xuống cạnh BC.
Giải: Áp dụng hệ thức

Hệ thức lượng trong tam giác vuông là một phần nhỏ trong hình học nhưng có vai trò lớn trong việc rút ngắn thời gian giải bài và tăng tính chính xác. Đây là mảnh ghép không thể thiếu trong hệ thống kiến thức trọng tâm thi vào 10 môn Toán, đặc biệt với những câu hình học yêu cầu tính toán hoặc chứng minh nhanh. Học sinh nên ghi nhớ các hệ thức, luyện tập nhiều bài toán mẫu để áp dụng linh hoạt trong các tình huống khác nhau.
6. Tỉ số lượng giác của góc nhọn
Đây là phần thường xuyên xuất hiện trong đề thi vào lớp 10, nhất là các bài yêu cầu tính độ dài cạnh, tính góc hoặc giải bài toán thực tế. Vì vậy, đây là một phần kiến thức trọng tâm thi vào 10 môn Toán mà học sinh cần đặc biệt chú ý, ôn tập kỹ và luyện tập đều đặn.
Tỉ số lượng giác của góc nhọn là các tỉ số của góc nhọn và các cạnh tương ứng xuất hiện trong các tam giác vuông.
- Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
- Tỉ số giữa cạnh kề và cạnh huyền được gọi là cos (cosin) của góc α, kí hiệu là cos α.
- Tỉ số giữa cạnh đối và cạnh kề được gọi là tan (tang) của góc α, kí hiệu là tan α.
- Tỉ số giữa cạnh kề và cạnh đối được gọi là cot (côtang) của góc α, kí hiệu là cot α.

Ví dụ: Cho tam giác ABC vuông tại A, gọi góc ACB là α.
 |
Góc α có:
Sin α = AB/BC (tỉ số cạnh đối với cạnh huyền) Cos α = AC/BC (tỉ số cạnh kề với cạnh huyền) Tan α = AB/AC (tỉ số cạnh đối với cạnh kề) Cot α = AC/AB (tỉ số cạnh kề với cạnh đối) |
Bảng giá trị tỉ số lượng giác của một số góc đặc biệt:

Ví dụ: Cho tam giác ABC, góc BAC bằng 90 độ, góc ACB bằng 30 độ, biết BC = 10cm. Tính AB, AC.

Ta có:
c = a.sinC
⇒ c = 10.sin30°
⇒ c = 10.1/2
⇒ c = AB = 5 (cm)
b = a.cosC
⇒ b = 10.cos30°
⇒ b = 10.√3/2
⇒ b = AC = 5√3 (cm)
Tỉ số lượng giác của góc nhọn không chỉ là phần trọng tâm trong chương trình lớp 9 mà còn là công cụ hữu ích để giải nhiều dạng bài hình học, toán thực tế trong đề thi vào 10. Đây là một mắt xích quan trọng trong hệ thống kiến thức trọng tâm thi vào 10 môn Toán, đặc biệt ở các câu hỏi hình học liên quan đến tam giác vuông.
7. Đường tròn
Những bài toán liên quan đến đường tròn tuy không dài nhưng lại đòi hỏi học sinh phải thật tinh tế trong việc quan sát hình, ghi nhớ tính chất và suy luận logic. Chính vì vậy, việc nắm chắc lý thuyết và kỹ năng giải toán về đường tròn là điều kiện bắt buộc trong quá trình ôn tập các kiến thức trọng tâm thi vào 10 môn Toán.
Khái niệm và tính chất cơ bản của đường tròn
- Đường tròn tâm O, bán kính R (R>0), ký hiệu là (O;R), là hình gồm tất cả các điểm cách điểm O một khoảng đúng bằng R.
- Một đường tròn được xác định hoàn toàn khi biết tâm và bán kính. Khi không quan tâm đến bán kính, chỉ cần ghi đường tròn tâm O là (O).
- Nếu A là một điểm nằm trên đường tròn (O) thì ta viết: A∈(O). Khi đó, có thể nói: Đường tròn (O) đi qua điểm A, hoặc điểm A nằm trên đường tròn (O).

Nhận xét vị trí tương đối giữa điểm và đường tròn:
- Điểm M nằm trên đường tròn (O;R) nếu OM=R
- Điểm M nằm trong đường tròn (O;R) nếu OM<R
- Điểm M nằm ngoài đường tròn (O;R) nếu OM>R
Tính đối xứng của đường tròn:
- Đường tròn là hình có tâm đối xứng. Tâm của đường tròn chính là tâm đối xứng của nó.
- Đường tròn cũng là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm của đường tròn là một trục đối xứng của đường tròn.
Ví dụ:
Tính bán kính khi biết đường kính
Một đường tròn có đường kính bằng 10 cm. Tính bán kính.

Tính độ dài dây cung khi biết khoảng cách từ tâm
Trong đường tròn tâm O, bán kính r=5 cm. Một dây cung AB cách tâm O một đoạn 3 cm. Tính độ dài dây AB.
Giải: Tam giác vuông tại trung điểm dây cung: OA² = OH² + AH² ⇒ 25 = 9 + AH² ⇒ AH = √16 = 4 ⇒ AB = 2 ⋅ AH = 8cm
Đường tròn là nền tảng của hàng loạt bài toán hình học trong đề thi tuyển sinh lớp 10 như tiếp tuyến, tam giác nội tiếp, chứng minh góc… Nắm chắc các khái niệm cơ bản và các tính chất quan trọng là chìa khóa để giải quyết các bài toán chính xác, ngắn gọn.
8. Tiếp tuyến của đường tròn
Học sinh không chỉ cần nắm lý thuyết về tiếp tuyến mà còn phải biết kết hợp với các yếu tố như tam giác, góc, đường tròn nội tiếp hoặc ngoại tiếp. Chính vì vậy, đây là một trong những kiến thức trọng tâm thi vào 10 môn Toán mà học sinh cần học chắc và luyện sâu.
Khái niệm: Tiếp tuyến của một đường tròn là đường thẳng chỉ có một điểm chung duy nhất với đường tròn – điểm đó gọi là tiếp điểm.
Một đường thẳng d là tiếp tuyến của đường tròn tâm O, bán kính R tại điểm M nếu và chỉ nếu:
![]()
Để nhận biết một đường thẳng là tiếp tuyến của một đường tròn ta có hai dấu hiệu sau:
- Đường thẳng và đường tròn chỉ có một điểm chung (định nghĩa tiếp tuyến).
- Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.

Ví dụ: Cho tam giác ABC có AB = 3cm; Ac = 4cm; BC = 5cm. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn
Lời giải:
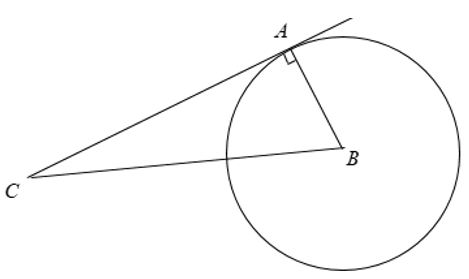 |
Ta có: AB² + AC² = BC²
⇒ ΔABC là tam giác vuông tại A. hay AC ⊥ AB Áp dụng dấu hiệu nhận biết của tiếp tuyến ta có: + AC với đường tròn (B) có một điểm chung là A. + Đường thẳng AC đi qua A và vuông góc với bán kính BA. ⇒ AC là tiếp tuyến của đường tròn (B; BA) |
Phần tiếp tuyến của đường tròn là công cụ then chốt để mở khóa nhiều bài toán phức tạp hơn trong đề thi vào lớp 10. Những tính chất như “tiếp tuyến vuông góc với bán kính”, “hai tiếp tuyến bằng nhau”… là nền tảng để chứng minh, tính toán và dựng hình. Học sinh lớp 9 muốn làm chủ phần hình học cần nắm chắc bản chất và thực hành đúng cách.
9. Góc với đường tròn
Một trong những nội dung thường gây nhầm lẫn nhất trong đề thi vào lớp 10 là góc với đường tròn. Từ góc nội tiếp, góc ở tâm đến góc tạo bởi tiếp tuyến và dây cung – mỗi dạng đều có tính chất riêng biệt nhưng liên quan chặt chẽ với cung tròn. Học sinh lớp 9 cần xác định đây là kiến thức trọng tâm thi vào 10 môn Toán, và luyện tập một cách hệ thống để không bị mất điểm đáng tiếc.
Các loại góc trong đường tròn và tính chất
| Góc ở tâm |
|
| Góc nội tiếp |
Ví dụ: Góc ACB là góc nội tiếp chắn cung AB |
| Góc tạo bởi tiếp tuyến và dây cung |
Ví dụ: Góc BAx là góc tạo bởi tia tiếp tuyến Ax bà dây cung AB |
Từ việc nhận diện góc đến tính số đo, học sinh cần nắm chắc bản chất từng loại góc và luyện tập thật nhiều để ghi nhớ công thức, tránh nhầm lẫn.
10. Các loại hình trong không gian
Ở phần cuối của chương trình hình học THCS, học sinh được tiếp cận với các hình khối trong không gian như hình hộp chữ nhật, hình lập phương, hình chóp, hình lăng trụ… Đây là những hình quen thuộc trong đời sống và thường xuất hiện trong đề thi dưới dạng bài tính diện tích xung quanh, thể tích, hoặc nhận biết hình không gian.
Hình hộp chữ nhật
- Có 6 mặt là hình chữ nhật.
- Các cạnh vuông góc, các mặt đối song song và bằng nhau.
Công thức:
- Thể tích:V = a⋅ b⋅ c
- Diện tích toàn phần: S = 2(ab+bc+ca)
Hình lập phương
Công thức:
- Thể tích: V = a³
- Diện tích toàn phần: S=6a²
Hình chóp tứ giác đều
Đáy là hình vuông, các cạnh bên bằng nhau, các mặt bên là tam giác cân.
Công thức:
Thể tích: V = 1/3 . S đáy . h
Hình lăng trụ đứng
- Hai đáy là đa giác bằng nhau và song song.
- Các cạnh bên vuông góc với đáy.
Công thức:
Thể tích: V = S đáy . h
Ví dụ: Tính thể tích hình hộp chữ nhật
Một hình hộp chữ nhật có kích thước a=4 cm, b=3 cm, c=5 cm. Tính thể tích và diện tích toàn phần.
Giải:
Thể tích: V = 4 ⋅ 3 ⋅ 5 = 60 cm³
Diện tích toàn phần: 
Các bài toán hình học không gian thường chiếm 1–2 điểm trong đề thi tuyển sinh vào 10. Với dạng bài chủ yếu là nhận biết, tính thể tích và diện tích, học sinh hoàn toàn có thể ăn trọn điểm nếu ghi nhớ công thức và trình bày cẩn thận.
Tổng kết
Ôn thi vào lớp 10 không chỉ là hành trình luyện đề, mà còn là quá trình học sinh tự hệ thống và làm chủ toàn bộ kiến thức trọng tâm thi vào 10 môn Toán. Từ căn thức đại số, phương trình – hàm số đến hình học phẳng và hình học không gian, mỗi chuyên đề đều có vai trò riêng trong việc xây nền vững chắc cho bài thi tuyển sinh.
Để việc ôn tập thêm hiệu quả và đúng hướng, học sinh có thể tham khảo bộ sách Ôn thi vào lớp 10 môn Toán (NXB Giáo dục Việt Nam) – tài liệu được biên soạn sát đề thi thực tế, phân dạng rõ ràng và có lời giải chi tiết từng bước.
Ngoài ra, đừng quên truy cập HEID để cập nhật thêm tài liệu, mẹo làm bài và lộ trình ôn luyện dành riêng cho học sinh lớp 9. HEID luôn đồng hành cùng bạn trên hành trình chinh phục cánh cửa vào lớp 10 với kết quả tốt nhất.







