Danh mục
ToggleLý thuyết trọng tâm ôn thi môn toán vào 10 là từ khóa quan trọng được nhiều người tìm kiếm, bởi đây là nền tảng cốt lõi nhưng thường bị học sinh coi nhẹ trong quá trình ôn luyện. Nhiều em chỉ tập trung luyện đề mà quên rằng không nắm chắc lý thuyết sẽ dễ dẫn đến hiểu sai bản chất bài toán, chọn nhầm hướng giải hoặc áp dụng công thức không chính xác. Một số em học trước quên sau, học thuộc mà không hiểu, khiến việc ghi nhớ trở nên áp lực và kém hiệu quả.
Trong bài viết này, HEID tổng hợp các kiến thức lý thuyết Toán trọng tâm ôn thi môn toán vào 10 bám sát chương trình lớp 9, được trình bày theo từng chuyên đề rõ ràng, ngắn gọn và dễ nhớ. Nội dung phù hợp để giáo viên sử dụng trong quá trình xây dựng giáo án ôn thi, đồng thời cũng là tài liệu hữu ích giúp học sinh hệ thống lại kiến thức, tự ôn tập một cách logic và khoa học.
Hy vọng bài viết sẽ là công cụ hỗ trợ đắc lực cho cả thầy và trò trong hành trình chinh phục kỳ thi vào lớp 10 đầy thử thách.

1. Tổng quan cấu trúc đề thi vào 10 môn Toán
Kỳ thi tuyển sinh vào lớp 10 môn Toán thường được tổ chức theo hình thức thi tự luận, yêu cầu học sinh trình bày lời giải chi tiết và logic. Cấu trúc đề thi nhìn chung ổn định qua các năm, gồm từ 5 đến 7 bài toán, được sắp xếp từ cơ bản đến nâng cao nhằm phân loại năng lực học sinh.
Hình thức thi
- Tự luận 100%: Học sinh phải trình bày rõ ràng từng bước giải, không được phép làm tắt.
- Một số địa phương có thể kết hợp 10–20% trắc nghiệm, nhưng chưa phổ biến.
Thời gian làm bài
- 90 phút, không kể thời gian phát đề.
- Học sinh cần rèn kỹ năng tính toán và quản lý thời gian hiệu quả để hoàn thành bài thi đúng hạn.

Phân bố kiến thức theo chương trình lớp 9
- Khoảng 80–90% nội dung đề thi tập trung vào kiến thức lớp 9, chủ yếu ở các chuyên đề: phương trình, hệ phương trình, căn thức, hàm số, bất phương trình, hình học phẳng.
- Một số câu hỏi yêu cầu vận dụng kiến thức lớp 8 và lớp 7, nhưng chỉ chiếm tỷ trọng nhỏ, thường là các kiến thức nền như: hằng đẳng thức, biểu thức đại số, hình học cơ bản.
Tỷ trọng kiến thức lớp 6–8
- Khoảng 10–20%, chủ yếu xuất hiện trong các bài toán mở rộng hoặc bài toán thực tế.
- Kiến thức lớp dưới giúp học sinh giải quyết nhanh các bước biến đổi, rút gọn, hoặc chứng minh đơn giản.
Việc nắm vững cấu trúc đề thi là bước đầu giúp học sinh lên kế hoạch ôn tập hợp lý và giáo viên phân bổ thời lượng giảng dạy phù hợp với từng dạng bài.
2. Lý thuyết trọng tâm ôn thi môn toán vào 10 – Lý thuyết Đại số trọng tâm
2.1 Căn bậc hai, hằng đẳng thức đáng nhớ
Căn bậc hai và các hằng đẳng thức là phần nền tảng xuyên suốt chương trình Toán THCS. Đây là công cụ không thể thiếu trong biến đổi biểu thức, giải phương trình và rút gọn căn thức.

Lý thuyết và công thức
-
Căn bậc hai: Với a ≥ 0, căn bậc hai của a là số x sao cho x² = a, ký hiệu là √a. Một số công thức cần ghi nhớ: √(a²) = |a|, √(ab) = √a × √b, √(a/b) = √a / √b (với b ≠ 0).
-
Hằng đẳng thức đáng nhớ:
-
(a + b)² = a² + 2ab + b²
-
(a − b)² = a² − 2ab + b²
-
a² − b² = (a − b)(a + b)
-
Nắm chắc các công thức trên sẽ giúp học sinh rút gọn biểu thức, xử lý nhanh các bài toán có chứa căn thức và hằng đẳng thức.
Ví dụ
Học sinh cần ghi nhớ các hằng đẳng thức và cách khai triển căn thức cơ bản. Đây là kỹ năng thiết yếu khi làm bài rút gọn biểu thức, giải phương trình và các bài toán nâng cao có chứa căn thức.
2.2 Phương trình – hệ phương
Phương trình và hệ phương trình là nội dung chiếm tỷ trọng lớn trong đề thi. Học sinh cần biết phân biệt các loại phương trình và vận dụng linh hoạt phương pháp giải.
Lý thuyết và công thức
-
Phương trình bậc nhất một ẩn: Có dạng ax + b = 0 (a ≠ 0), nghiệm duy nhất là x = −b/a.
-
Phương trình chứa ẩn ở mẫu: Cần tìm điều kiện xác định trước khi giải.
-
Phương trình chứa căn: Dùng phương pháp bình phương hai vế, đặt ẩn phụ hoặc loại căn.
-
Hệ phương trình bậc nhất hai ẩn: Gồm hai phương trình có dạng:
{a1x+b1y=c1a2x+b2y=c2
Các phương pháp giải thường dùng: thế, cộng đại số, sử dụng biểu đồ.
Việc nhận diện nhanh dạng phương trình và chọn đúng phương pháp giải sẽ giúp học sinh tiết kiệm thời gian và tránh sai sót.
Ví dụ
Nắm vững từng loại phương trình, cách phân tích đề và chọn đúng phương pháp giải là yếu tố then chốt để làm nhanh và chính xác.
2.3 Hàm số và đồ thị
Hàm số và đồ thị giúp mô tả mối quan hệ giữa hai đại lượng và là nội dung thường xuất hiện trong đề thi, đặc biệt là các bài toán vẽ đồ thị, tìm tọa độ giao điểm, hoặc tìm giá trị lớn nhất – nhỏ nhất.
Lý thuyết và công thức
-
Phương trình bậc nhất một ẩn: Có dạng ax + b = 0 (a ≠ 0), nghiệm duy nhất là x = −b/a.
-
Phương trình chứa ẩn ở mẫu: Cần tìm điều kiện xác định trước khi giải.
-
Phương trình chứa căn: Dùng phương pháp bình phương hai vế, đặt ẩn phụ hoặc loại căn.
-
Hệ phương trình bậc nhất hai ẩn: Gồm hai phương trình có dạng:
{a1x+b1y=c1a2x+b2y=c2
Các phương pháp giải thường dùng: thế, cộng đại số, sử dụng biểu đồ.
Việc nhận diện nhanh dạng phương trình và chọn đúng phương pháp giải sẽ giúp học sinh tiết kiệm thời gian và tránh sai sót.
Ví dụ
Học sinh cần thành thạo cách lập bảng giá trị, vẽ đồ thị chính xác và xác định đỉnh parabol để làm nhanh các dạng bài yêu cầu phân tích hàm số.
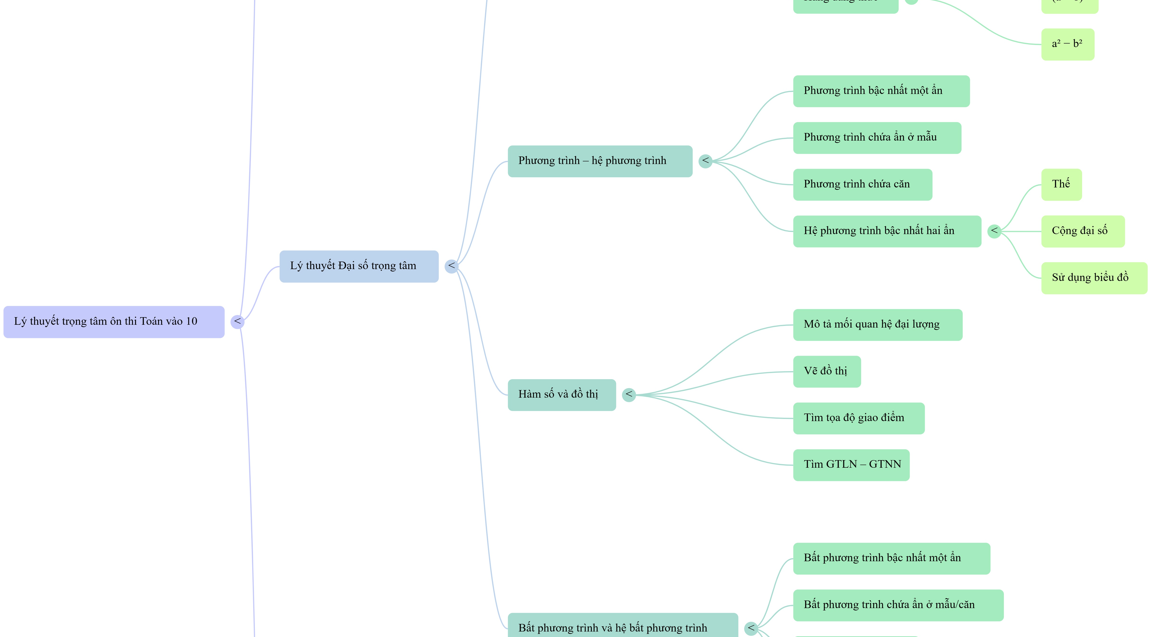
Tải Mindmap đầy đủ về Lý thuyết ôn thi toán vào 10 tại Link GG Drive
2.4 Bất phương trình và hệ bất phương trình
Bất phương trình xuất hiện trong các đề kiểm tra năng lực và đề thi phân loại. Học sinh cần hiểu rõ khái niệm, cách giải và biểu diễn nghiệm trên trục số.
Lý thuyết và công thức
- Bất phương trình bậc nhất một ẩn: Có dạng
ax+b>0,
ax+b<0,
ax+b≥0, hoặc ax+b≤0.
Cách giải tương tự phương trình, lưu ý đổi chiều dấu bất phương trình khi nhân hoặc chia hai vế với số âm.
-
Bất phương trình chứa ẩn ở mẫu hoặc căn: Cần xác định điều kiện xác định, sau đó biến đổi tương đương để tìm nghiệm.
-
Hệ bất phương trình: Là hai hoặc nhiều bất phương trình cùng lúc. Nghiệm là phần giao của các miền nghiệm.
Kỹ năng biểu diễn nghiệm trên trục số và tìm miền thỏa mãn là yếu tố quan trọng để làm đúng các bài toán phân loại.
Ví dụ
Bất phương trình không khó nếu học sinh giải từng bước và luyện kỹ năng biểu diễn nghiệm chính xác.
3. Lý thuyết hình học trọng tâm

3.1 Hệ thức lượng trong tam giác vuông
Đây là phần kiến thức nền trong hình học lớp 9, thường xuyên xuất hiện trong đề thi với các dạng bài tính độ dài, chứng minh, hoặc ứng dụng vào thực tế.
Lý thuyết và công thức
-
Định lý Pytago: Trong tam giác vuông có cạnh huyền c, hai cạnh góc vuông là a và b, ta có:
-
Tỉ số lượng giác trong tam giác vuông:
-
-
-
-
-
Hệ thức lượng:
-
(đường cao h ứng với cạnh huyền chia huyền thành hai đoạn m và n)
-
-
Việc nắm chắc các hệ thức này giúp học sinh xử lý hiệu quả các bài toán tính cạnh, tính góc và các bài toán thực tế.
Ví dụ
Cho tam giác vuông tại A, AB = 3 cm, AC = 4 cm. Tính BC.
→ Áp dụng Pytago:
Nắm vững hệ thức lượng giúp học sinh giải nhanh các bài toán tính độ dài cạnh, góc và là bước đệm quan trọng cho các bài hình nâng cao.
3.2 Quan hệ giữa các yếu tố trong tam giác
Trong tam giác, mối quan hệ giữa các yếu tố như cạnh, góc, đường cao, trung tuyến, trung trực,… là nền tảng để giải quyết nhiều dạng toán hình học cơ bản và nâng cao.
Lý thuyết và công thức
- Tổng ba góc trong một tam giác luôn bằng 180 độ.
- Trong tam giác cân: hai cạnh bằng nhau thì hai góc đối diện cũng bằng nhau.
- Trong tam giác vuông:
- Có một góc bằng 90 độ.
- Áp dụng định lý Pytago để tính cạnh.
- Định lý sin và cos dùng trong các bài toán tam giác không vuông.
Ví dụ
Cho tam giác ABC vuông tại A, biết AB = 6 cm, AC = 8 cm. Tính BC.
→ Áp dụng định lý Pytago:
Việc ghi nhớ các mối quan hệ trong tam giác giúp học sinh định hướng cách làm nhanh chóng, tránh mất điểm ở những câu cơ bản.
3.3 Đường tròn và góc nội tiếp
Các bài toán liên quan đến đường tròn, góc nội tiếp thường là phần phân loại trong đề thi vào 10. Đây là phần học sinh hay mắc lỗi nếu không nắm rõ tính chất.
Lý thuyết và công thức
- Góc nội tiếp chắn nửa đường tròn thì bằng 90 độ.
- Số đo góc nội tiếp bằng nửa số đo cung bị chắn.
- Hai tiếp tuyến cắt nhau tại một điểm ngoài đường tròn tạo thành hai tam giác cân.
Ví dụ
Cho đường tròn tâm O, dây AB = đường kính. M là điểm trên đường tròn sao cho tam giác AMB được tạo thành.
→ Khi đó, góc AMB = 90 độ (do chắn nửa đường tròn).
Học sinh cần luyện nhiều dạng bài vẽ hình và suy luận theo tính chất để đạt điểm tối đa ở phần này.
3.4 Tứ giác nội tiếp
Tứ giác nội tiếp là dạng hình đặc biệt có nhiều tính chất đặc trưng, thường xuất hiện trong các bài toán chứng minh hình học.
Lý thuyết và công thức
- Tổng hai góc đối trong tứ giác nội tiếp bằng 180 độ.
- Nếu tứ giác nội tiếp thì tồn tại một đường tròn đi qua bốn đỉnh.
- Định lý: Tứ giác ABCD nội tiếp đường tròn ⇔ ∠A + ∠C = 180° (hoặc ∠B + ∠D = 180°)
Ví dụ
Cho tứ giác ABCD nội tiếp đường tròn, biết ∠A = 110°. Tính ∠C.
→ ∠C = 180° – ∠A = 70°
Việc nhận diện nhanh tứ giác nội tiếp và áp dụng đúng công thức sẽ giúp học sinh xử lý tốt các bài chứng minh và tìm góc.
3.5 Các bài toán thực tế hình học
Một số đề thi vào 10 có dạng toán thực tế, yêu cầu vận dụng hình học vào tính toán thực tiễn: chiều cao, khoảng cách, diện tích…
Lý thuyết và công thức
- Áp dụng hệ thức lượng trong tam giác vuông.
- Sử dụng công thức diện tích: tam giác (½ × đáy × chiều cao), hình tròn, hình chữ nhật,…
- Tính tỉ lệ giữa các đoạn thẳng, so sánh độ dài.
Ví dụ
Một cột điện cao 6m tạo bóng dài 8m trên mặt đất. Tính khoảng cách từ đỉnh cột đến điểm cuối bóng.
→ Tam giác vuông, áp dụng Pytago:
Bên cạnh tài liệu ôn tập cá nhân, giáo viên và học sinh có thể tham khảo thêm sách “Ôn thi vào lớp 10 môn Toán” do Nhà xuất bản Giáo dục Việt Nam phát hành. Đây là tài liệu chính thống, bám sát chương trình THCS, tổng hợp đầy đủ lý thuyết trọng tâm, bài tập vận dụng, đề minh họa và hướng dẫn giải chi tiết – rất hữu ích cho cả việc học trên lớp lẫn ôn luyện tại nhà.
Hy vọng bài viết này sẽ là trợ thủ đắc lực cho thầy cô trong quá trình xây dựng giáo án, và là kim chỉ nam giúp các em học sinh ôn thi hiệu quả, vững vàng chinh phục kỳ thi vào lớp 10 với kết quả tốt nhất.





