Danh mục
ToggleMôn Toán trong kỳ thi tốt nghiệp THPT chưa bao giờ là “dễ thở”. Điều khiến nhiều học sinh mất điểm nhất không phải là bài toán quá lạ, mà là những lỗi “rất quen”: quên công thức đạo hàm, nhớ nhầm tích phân, áp sai định lý lượng giác. Vì vậy, nếu bạn đang ôn thi nước rút mà chưa có bộ công thức Toán ôn thi tốt nghiệp THPT bỏ túi, thì hành trang vào phòng thi vẫn còn thiếu một mảnh rất quan trọng.
Trong bài viết này, HEID sẽ mang đến trọn bộ công thức Toán ôn thi tốt nghiệp THPT được chọn lọc kỹ lưỡng, đi kèm mẹo học hiệu quả và ví dụ thực hành – giúp bạn tự tin xử lý đề trắc nghiệm trong thời gian ngắn nhất. Đây không chỉ là “bảng công thức” thông thường, mà là kim chỉ nam giúp bạn về đích an toàn và vững vàng trong kỳ thi sắp tới.

1. Tổng hợp công thức Toán ôn thi tốt nghiệp THPT
Kỳ thi tốt nghiệp THPT chủ yếu tập trung vào các kiến thức lớp 12, nhưng cũng tích hợp một phần nhỏ kiến thức lớp 10, 11. Để giúp bạn ôn tập hiệu quả, dưới đây là bộ công thức toán ôn thi tốt nghiệp THPT đã được hệ thống hóa thành 9 chuyên đề trọng tâm. Mỗi phần đều đi kèm với những công thức bắt buộc phải nhớ và ứng dụng thực tế.
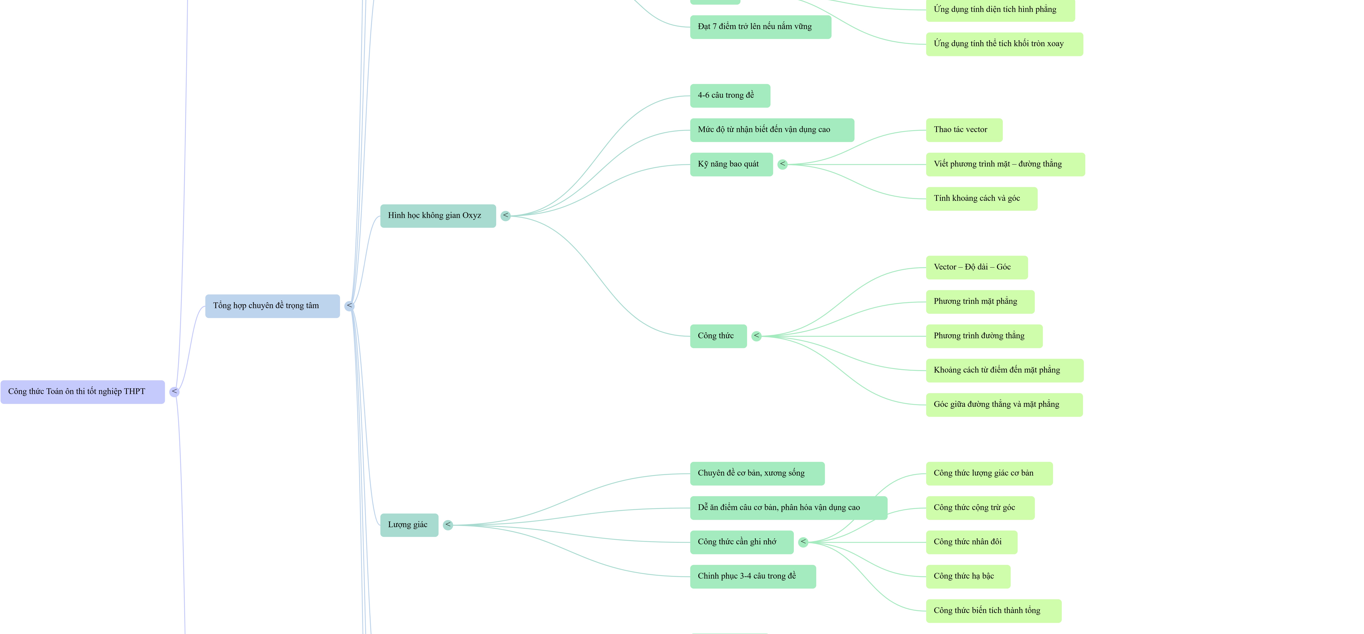
Tải Mindmap đầy đủ về Công thức toán ôn thi tốt nghiệp trung học phổ thông tại Link GG Drive
1.1 Hàm số – Đạo hàm – Tiếp tuyến
Chuyên đề hàm số- đạo hàm – tiếp tuyến luôn xuất hiện chắc chắn sẽ luôn xuất hiện trong đề thi môn Toán THPT Quốc gia. Đây là phần có độ phân hóa từ cơ bản đến nâng cao, bao gồm:
- Xét tính đơn điệu
- Tìm cực trị
- Giải phương trình tiếp tuyến
- Tìm tham số để hàm số thỏa mãn điều kiện cho trước
- Nhận dạng đồ thị
Vì vậy, việc nắm chắc công thức toán ôn thi tốt nghiệp THPT trong chuyên đề này là bắt buộc nếu bạn muốn đạt điểm trung bình – khá trở lên.
Các công thức đạo hàm cơ bản cần nhớ
- Đạo hàm của các hàm cơ bản

- Đạo hàm của hàm hợp: (f(g(x)))′=f′(g(x))⋅g′(x)
- Đạo hàm các phép toán:
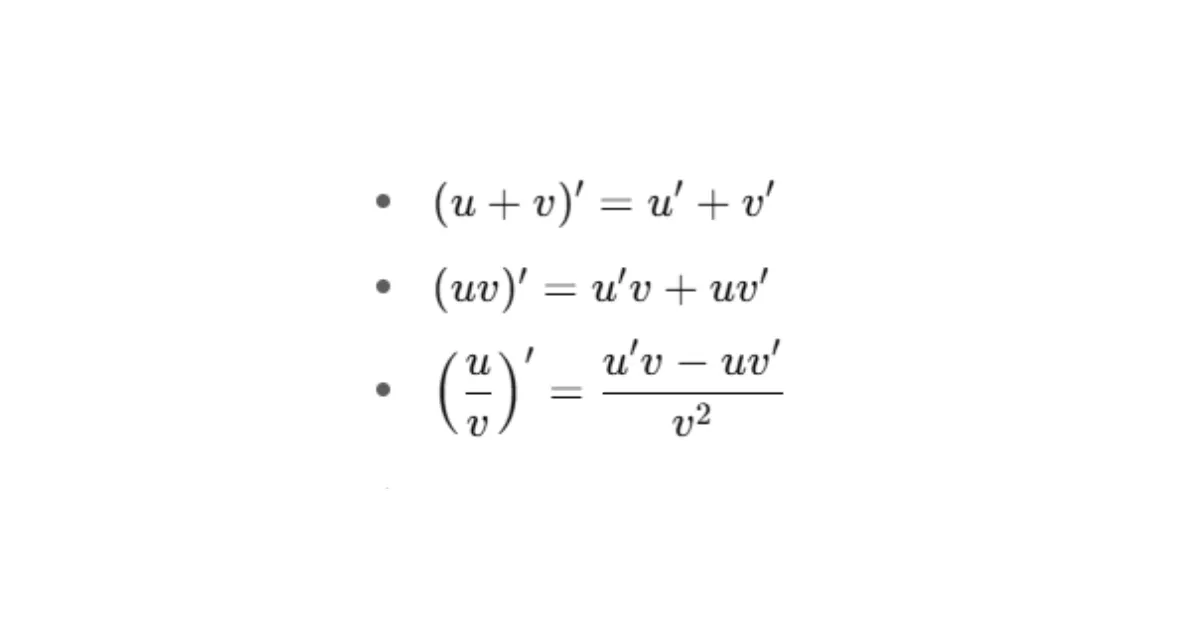
Xét tính đơn điệu – tìm cực trị

Công thức tiếp tuyến của đồ thị hàm số

Mẹo làm bài nhanh
-
Với bài tìm số cực trị → chỉ cần giải nhanh f′(x)=0 và đếm số lần đổi dấu
-
Với bài so sánh cực trị → thay giá trị vào hàm số để so sánh
-
Với bài tìm tiếp tuyến thỏa mãn điều kiện → áp dụng công thức tổng quát rồi thay trực tiếp
Nắm chắc đạo hàm giúp bạn chinh phục 15–20% đề thi, nên đừng học rời rạc mà hãy kết hợp công thức với luyện đềbởi đây luôn là phần mở đầu quan trọng trong mọi bảng công thức toán ôn thi tốt nghiệp THPT.
1.2 Mũ – Logarit
Mũ và logarit là một trong những chuyên đềcông thức ôn thi Toán tốt nghiệp THPT, tập trung vào 2 dạng chính:
- Biến đổi biểu thức
- Giải phương trình – bất phương trình
Hệ thống công thức mũ – logarit cần nhớ
- Công thức lũy thừa (mũ):

- Công thức logarit:

- Mối quan hệ giữa mũ và logarit:

Ví dụ
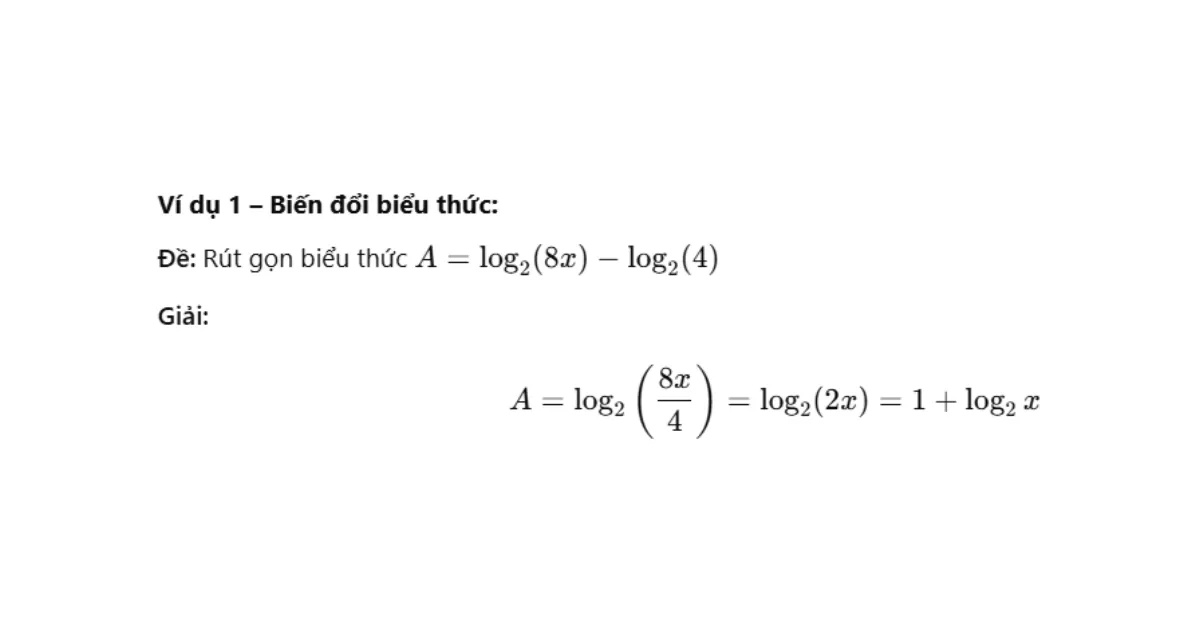

Mũ và logarit là phần “dễ ăn điểm” nếu nắm vững các công thức toán ôn thi tốt nghiệp THPT và biết cách biến đổi linh hoạt.
1.3 Nguyên hàm – Tích phân – Ứng dụng hình học
Nguyên hàm – tích phân là một trong những chuyên đề chiếm tỷ lệ điểm cao nhất trong đề thi tốt nghiệp THPT môn Toán với mức độ trải đều từ nhận biết, thông hiểu đến vận dụng cao. Các câu hỏi xoay quanh:
- Tính nguyên hàm cơ bản
- Tính tích phân xác định
- Ứng dụng tính diện tích hình phẳng
- Ứng dụng tính thể tích khối tròn xoay
Các công thức nguyên hàm cần nhớ

Công thức tích phân
- Tính tích phân xác định:

- Tính chất tích phân:
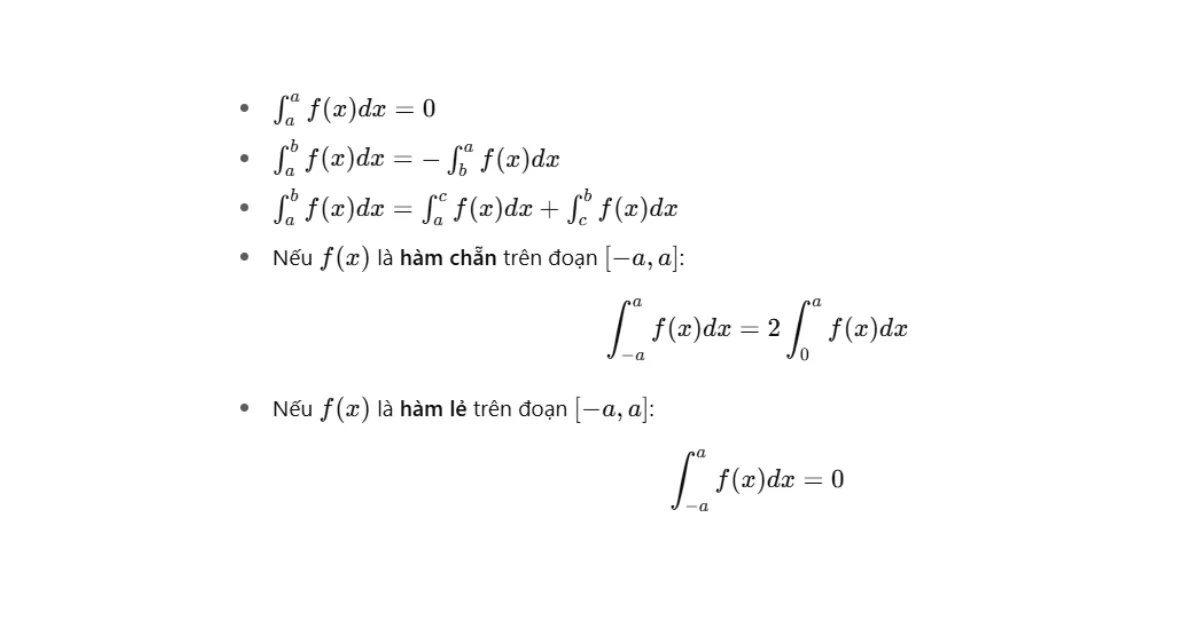
Ứng dụng hình học của tích phân
- Tính diện tích hình phẳng:
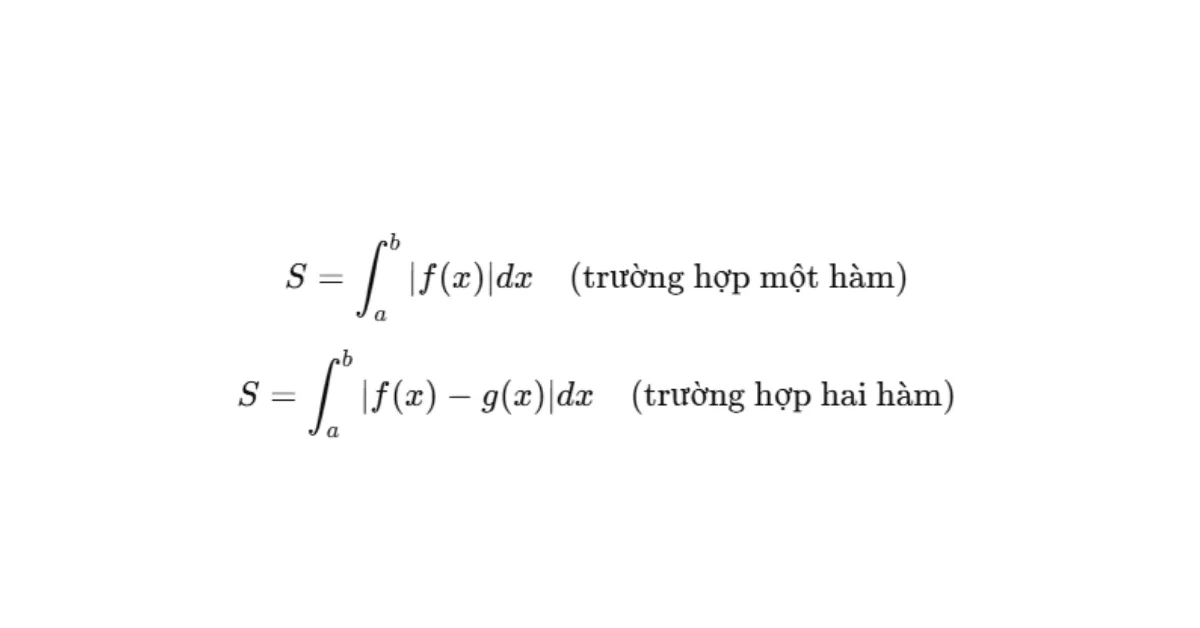
Ví dụ:

- Tính thể tích khối trong xoay:
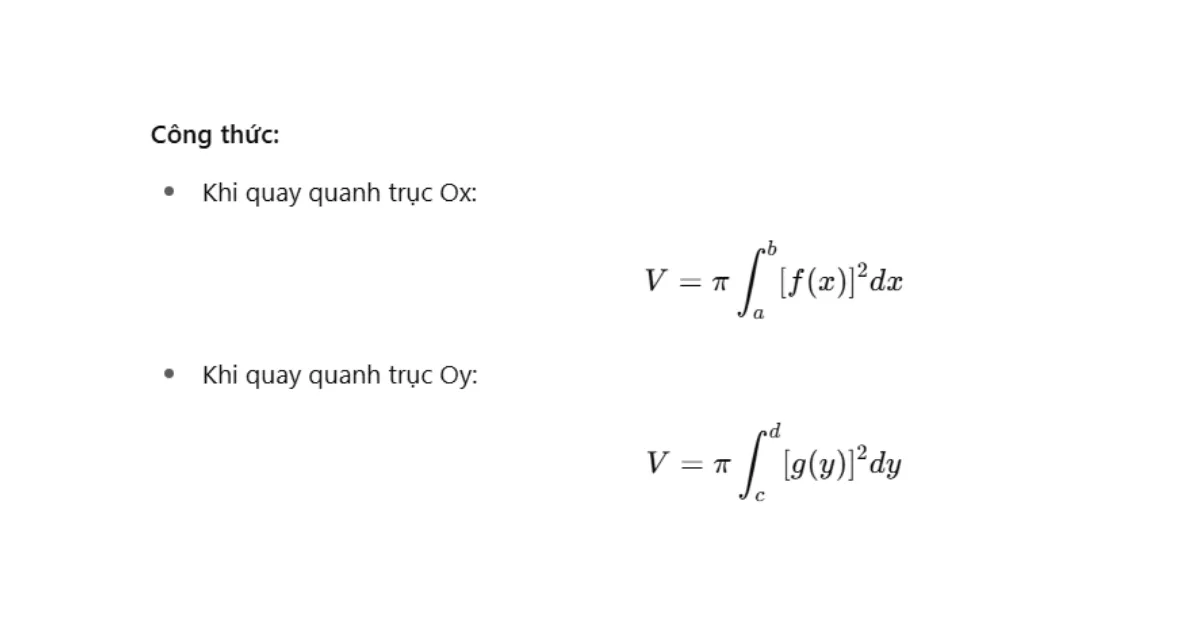
Ví dụ:

Nguyên hàm – tích phân là phần kiến thức chiếm tỷ trọng điểm cao trong đề thi, với các dạng bài từ cơ bản đến ứng dụng hình học, vì vậy nắm vững công thức, luyện tập thường xuyên và hiểu bản chất sẽ giúp bạn dễ dàng đạt từ 7 điểm trở lên trong kỳ thi tốt nghiệp THPT.
1.4 Hình học không gian Oxyz
Hình học không gian Oxyz là một chuyên đề “nhỏ nhưng có võ” trong đề thi tốt nghiệp THPT. Tuy số lượng câu hỏi không nhiều, thường từ 4 đến 6 câu, nhưng mức độ trải đều từ nhận biết đến vận dụng cao, bao quát nhiều kỹ năng: từ thao tác vector, viết phương trình mặt – đường thẳng, đến tính khoảng cách và góc.
Công thức hình học không gian
- Vector – Độ dài – Góc

- Phương trình mặt phẳng
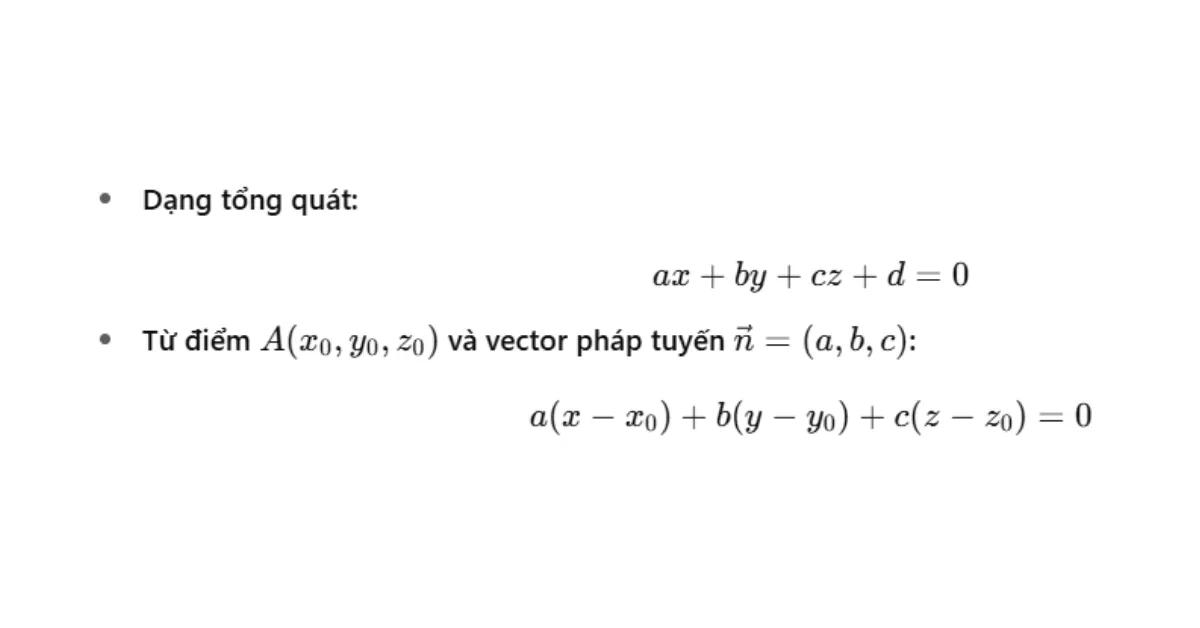
- Phương trình đường thẳng

Công thức tính khoảng cách – góc
- Khoảng cách từ điểm đến mặt phẳng

- Góc giữa đường thẳng và mặt phẳng

Ví dụ minh họa

Hình học không gian Oxyz là chuyên đề vừa chắc điểm, vừa giúp nâng cao tư duy không gian nếu ôn đúng cách. Đừng học thuộc lòng công thức rời rạc – hãy luyện bài tập thường xuyên để tăng phản xạ và tư duy hình học.
1.5 Lượng giác
Lượng giác là một trong những chuyên đề cơ bản nhưng “xương sống” trong công thức toán ôn thi tốt nghiệp THPT. Đây là phần vừa dễ ăn điểm ở câu cơ bản, vừa có thể tạo phân hóa ở mức vận dụng cao nếu bạn ôn tập chắc và hiểu bản chất.
Bảng công thức lượng giác cần ghi nhớ
- Công thức lượng giác cơ bản

- Công thức cộng trừ góc

- Công thức nhân đôi
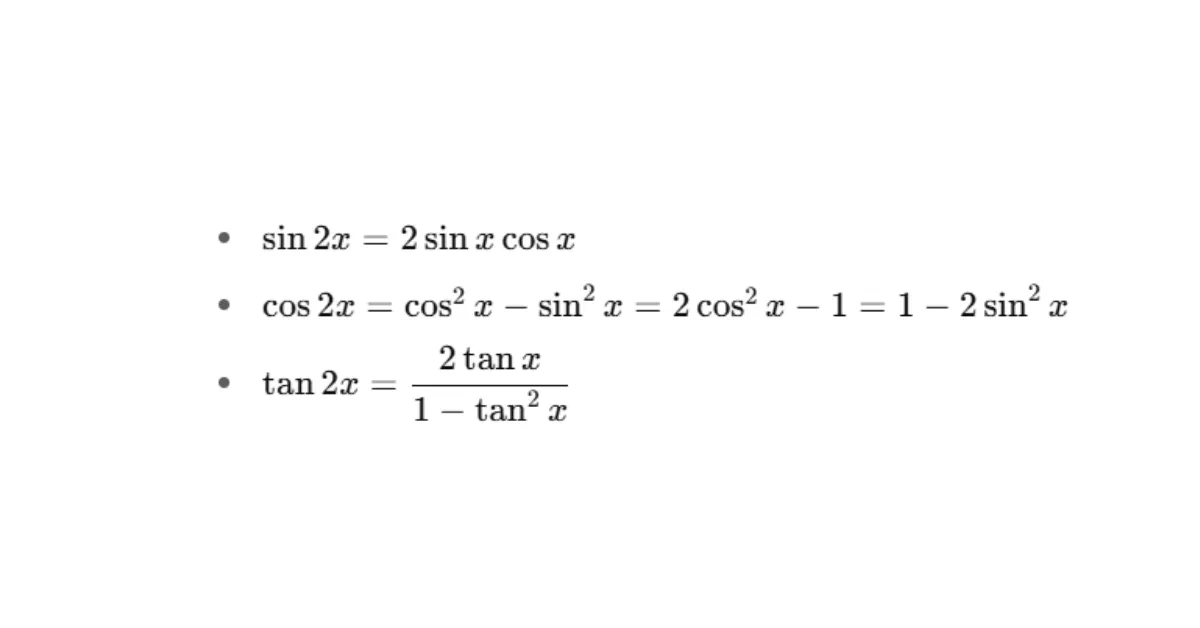
- Công thức hạ bậc
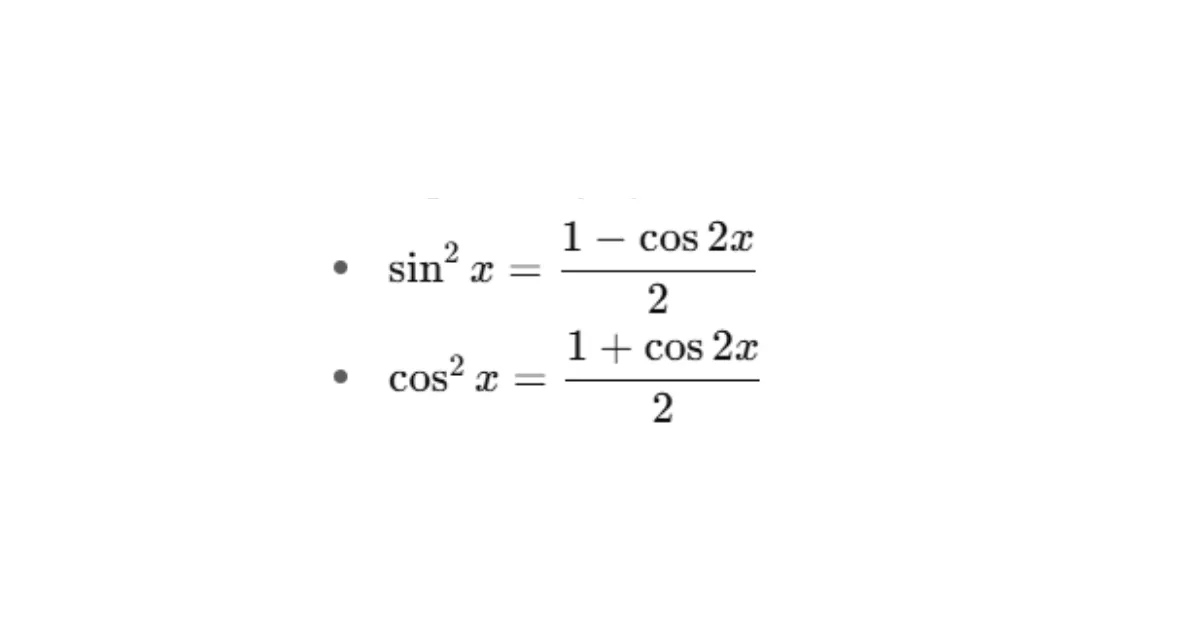
- Công thức biến tích thành tổng
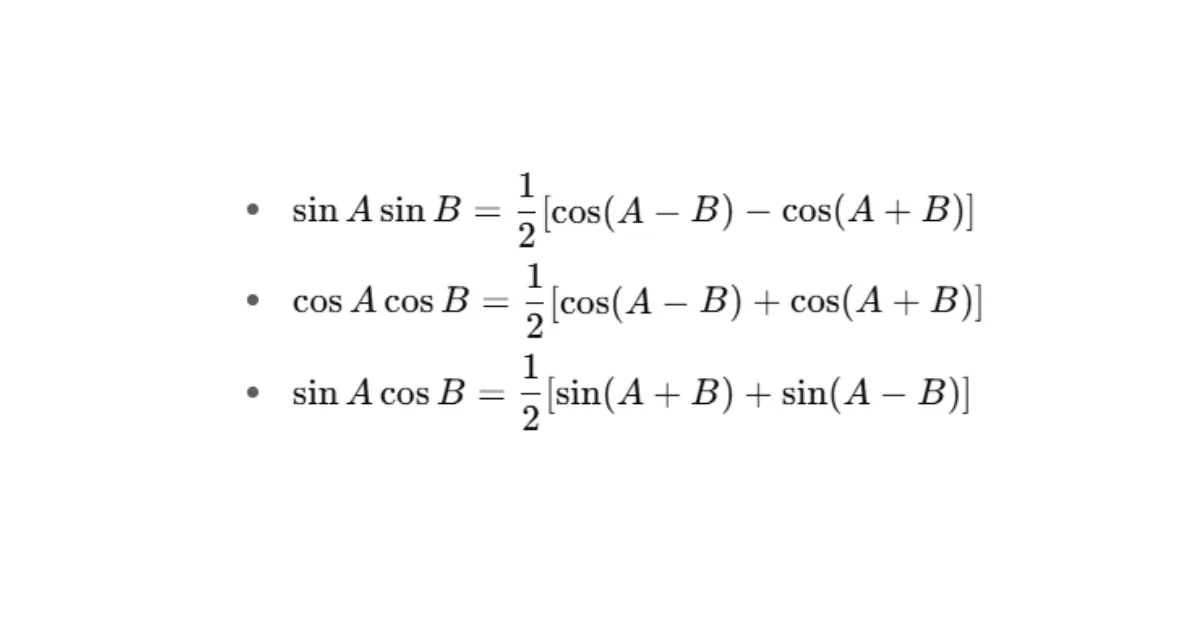
Ví dụ

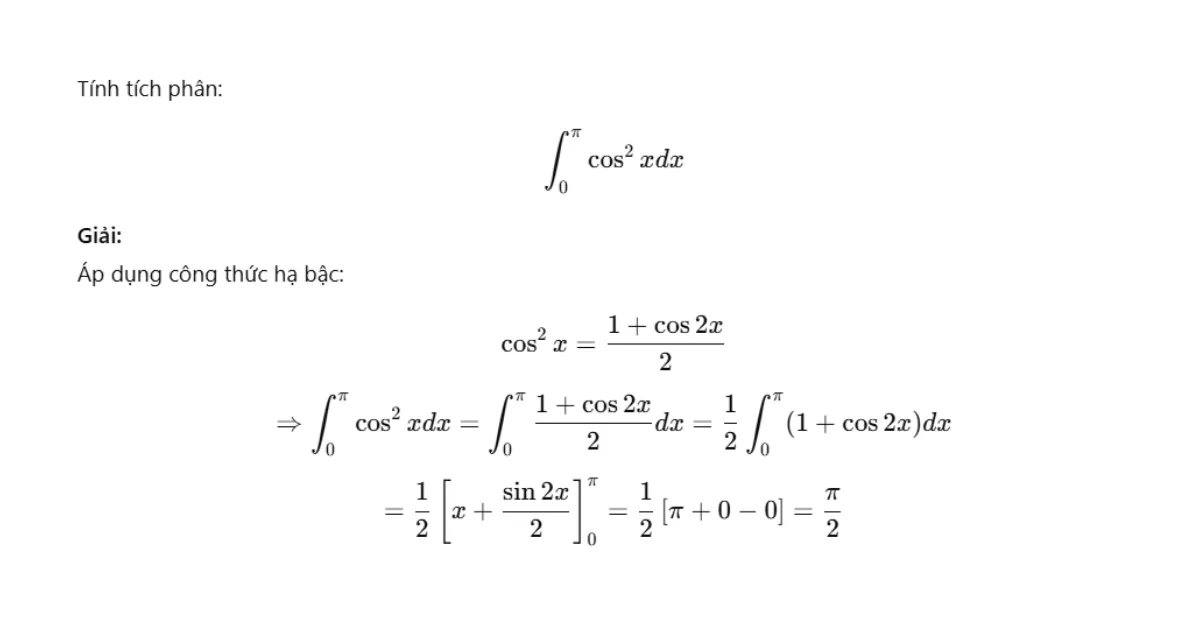
Lượng giác không khó, chỉ khó nếu bạn học nó như một dãy số khô khan. Vì vậy, hãy học lượng giác một cách thông minh và có chiến lược – và bạn sẽ thấy mình dễ dàng chinh phục được 3–4 câu lượng giác trong đề thi chính thức.
1.6 Tổ hợp – Xác suất
Tổ hợp và xác suất là một chuyên đề xuất hiện từ 2 đến 3 câu trong đề thi tốt nghiệp THPT, mức độ chủ yếu là hiểu và vận dụng. Dù số lượng câu hỏi ít, nhưng đây là phần học sinh có thể ghi điểm trọn vẹn nếu nhớ đúng công thức và luyện đúng dạng.
Công thức trọng tâm


Dạng bài và ví dụ minh họa
Dạng 1: Tính số cách chọn – sắp xếp (thuần tổ hợp – chỉnh hợp – hoán vị)
Có 7 học sinh, chọn 3 bạn để trao thưởng, không xét thứ tự. Hỏi có bao nhiêu cách?
Giải:
Chọn không thứ tự ⇒ dùng tổ hợp:
Dạng 2: Chọn theo điều kiện (ít nhất – nhiều nhất – có ràng buộc)
Từ 5 học sinh nam và 4 học sinh nữ, chọn 3 người sao cho có ít nhất 1 nữ.
Giải:
Tổng số cách chọn 3 người:
Số cách không có nữ: chọn 3 nam trong 5 nam →
⇒ Số cách có ít nhất 1 nữ:
Dạng 3: Tính xác suất (thường đi kèm tổ hợp)
Một lớp có 4 nam và 6 nữ. Chọn ngẫu nhiên 3 người. Tính xác suất chọn được toàn nữ.
Giải:
Tổng số cách chọn 3 người:
Số cách chọn 3 nữ trong 6 nữ:
Dạng 4: Xác suất trong bốc thăm – chia nhóm – rút bài
Có 10 tấm thẻ ghi số từ 1 đến 10. Chọn ngẫu nhiên 1 thẻ. Tính xác suất để thẻ có số chia hết cho 3.
Giải:
Các số chia hết cho 3 là: 3,6, 9
Tổng số thẻ: 10
Tổ hợp – xác suất không phải là phần gây khó, nhưng dễ mất điểm nếu nhầm lẫn giữa các khái niệm như chọn có thứ tự hay không, sắp xếp hay chia nhóm. Đây là một trong những chuyên đề “dễ kiếm điểm” nếu sĩ tử nắm chắc công thức cơ bản và làm quen với các tình huống thường gặp.
1.7 Hình học phẳng – Đường tròn, Elip, Hyperbol
Chuyên đề Hình hoc phẳng – Đường trong, Elip, Hyperbol chủ yếu kiểm tra khả năng nhận diện và xử lý nhanh các phương trình dạng chuẩn: tìm tâm, bán kính, độ dài trục, tiêu cự, hoặc xác định dạng tiếp xúc giữa hai đường. Đề bài không đánh đố – nếu bạn học đúng công thức, thì điểm nằm chắc trong tay.
Đường tròn
-
Phương trình đường tròn có tâm I (a,b) và bán kính R>0:
-
Nếu phương trình có dạng khai triển:
thì:
Elip

Hyperbol

Dạng bài thường gặp
- Xác định tâm và bán kính của đường tròn từ phương trình
Ví dụ:
Tìm tâm và bán kính của đường tròn:
Giải:
Nhóm x, y:
Bổ sung bình phương:
=> Tâm I (2, -1), bán kính R=5
- Viết phương trình elip/hyperbol
Ví dụ:
Viết phương trình elip có trục lớn nằm trên Ox, độ dài trục lớn 10, trục nhỏ 8
Giải:
→ Phương trình elip:
Ôn tập thật kĩ công thức trên sẽ giúp các học sinh làm bài một cách hiệu quả và không mất điểm đáng tiếc.
1.8 Giá trị lớn nhất – Giá trị nhỏ nhất – Bất đẳng thức
Tìm giá trị lớn nhất – nhỏ nhất (GTLN – GTNN) là dạng bài giúp phân loại học sinh, kiểm tra khả năng tư duy biến đổi, xét dấu đạo hàm, phân tích biểu thức… Nếu nắm được phương pháp và luyện đề đầy đủ, học sinh hoàn toàn có thể xử lý phần này nhanh và chính xác.
Các phương pháp tìm GTLN – GTNN
- Dùng đạo hàm
Đây là cách phổ biến nhất trong đề thi.
Các bước cơ bản:
-
Tính đạo hàm hàm sốf(x)
- Giải phương trình f'(x)=0 để tìm các điểm nghi ngờ là cực trị
- Lập bảng biến thiên hoặc xét dấu f'(x)
- So sánh giá trị f(x) tại các điểm cực tri và tại biên của đoạn xác định để chọn GTLN – GTNN
Ví dụ:

- Dùng bất đẳng thức (Cauchy – AM-GM – Bunhiacopxki)
Khi biểu thức phức tạp (chứa căn, phân thức, tích), không tiện dùng đạo hàm, thì dùng bất đẳng thức là phương pháp tối ưu.

- Dùng biến đổi lượng giác (với biểu thức chứa sin, cos)

Mẹo ghi nhớ
- Nếu đề yêu cầu tìm GTLN/GTNN trên đoạn kín, luôn xét biên (giá trị tại 2 đầu mút)
- Với biểu thức chứa căn hoặc phân thức → nghĩ đến bất đẳng thức AM–GM, Cauchy
- Nếu biểu thức chứa
sinx,
cosx → hãy liên hệ ngay với giá trị cực đại cực tiểu của tổ hợp lượng giác
- Không cần lập bảng biến thiên nếu hàm số chỉ đơn giản và có 1 hoặc 2 nghiệm đạo hàm → chỉ cần tính giá trị trực tiếp
Nếu nắm chắc các phương pháp này, học sinh có thể xử lý nhanh và chính xác 2–3 câu trong đề, nâng điểm thi rõ rệt mà không mất nhiều thời gian.
Trên đât là tổng hợp 8 chuyên đề công thức Toán ôn thi tốt nghiệp THPT trọng tâm mà học sinh cần ghi nhớ. Bất bì công thức và bài tập nào cũng sẽ là cơ hội để sĩ tử ăn điểm và hoàn thành bài thi tốt nhất. Học tập ngay hôm nay và ứng dụng thực tế với các đề luyện để nắm vững một cách chắc chắn.
2. Tài liệu hỗ trợ học công thức Toán ôn thi tốt nghiệp THPT
Để học các công thức trên một cách hiệu quả nhất, không thể nào thiếu đi tài liệu đi kèm với các đề thi phong phú nhằm giúp học sinh áp dụng tốt nhất.
Vậy đâu là công cụ hữu ích đó? Cùng khám phá ngay dưới đây nhé!
2.1 Sách “Hướng dẫn ôn thi tốt nghiệp Trung học phổ thông môn Toán”
Tài liệu “Hướng dẫn ôn thi tốt nghiệp THPT môn Toán” được biên soạn dành riêng cho học sinh lớp 12 trong giai đoạn nước rút, nhằm hỗ trợ quá trình ôn luyện hiệu quả, có định hướng và đúng trọng tâm. Nội dung sách được xây dựng bám sát cấu trúc và ma trận đề minh họa kỳ thi tốt nghiệp THPT năm 2025 do Bộ Giáo dục và Đào tạo công bố.
Ưu điểm vượt trội:
- Bám sát cấu trúc và ma trận đề minh họa năm 2025 của Bộ GD&ĐT và các Sở GD&ĐT các tỉnh thành phố.
- Hệ thống hóa kiến thức theo chuyên đề: hàm số, mũ – logarit, tích phân, hình học không gian, xác suất…
- Câu hỏi luyện tập đa dạng, phân tầng từ nhận biết đến vận dụng cao.
- Phân tích bài toán trước khi giải, giúp rèn tư duy và kỹ năng xử lý đề.
- Giải chi tiết, có nhận xét và mẹo làm bài, tránh sai sót thường gặp.
- Đề luyện tập phong phú, mô phỏng sát đề thi thật, hỗ trợ tự đánh giá năng lực.
Đây sẽ không chỉ là bộ tài liệu hữu ích cho học sinh mà còn là nguồn tham khảo giá trị cho giáo viên trong quá trình giảng dạy, định hướng ôn tập và ra đề luyện thi.
Tham khảo ngay tại đây

2.2 Đề luyện thi trực tuyến
Một tài liệu nữa mà học sinh không thể bỏ qua để ôn tập các công thức toán ôn thi tốt nghiệp THPT đó chính là các đề luyện thi trực tuyến.
Với những đề luyện này, học sinh có thể học ở bất cứ đâu một cách chủ động, làm bài và nhận điểm số ngay trong tích tắc với kết quả đánh giá cụ thể chi tiết. Các bạn có thể tham khảo Onthi.hoclieu.vn với 10+ đề thi trực tuyến chất lượng với cả dạng bài trắc nghiệm và tự luận để học sinh rèn cách ghi nhớ công thức và áp dụng như thi thật.

Hãy lựa chọn cho mình tài liệu phù hợp và sử dụng ngay hôm nay để rút ngắn thời gian ôn luyện nhé.
3. Kết luận
Ôn thi tốt nghiệp THPT môn Toán không chỉ là việc luyện đề miệt mài, mà còn là quá trình nắm chắc nền tảng kiến thức – trong đó, hệ thống công thức chính là chiếc “xương sống” không thể thiếu. Dù bạn là người học theo tư duy hay học theo mẹo, thì một bộ công thức toán ôn thi tốt nghiệp THPT được tổng hợp đầy đủ, rõ ràng và có hệ thống vẫn luôn là hành trang quan trọng giúp bạn tăng tốc ở giai đoạn nước rút.
Khi công thức không còn là thứ phải “nhớ”, mà trở thành “thói quen sử dụng” trong mỗi câu hỏi, bạn sẽ thấy việc chinh phục đề thi Toán trở nên nhẹ nhàng hơn rất nhiều.
Chúc sĩ tử ôn tập thật hiệu quả – chiến thắng mọi con số – chinh phục mọi ước mơ!





