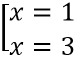Với khối lượng kiến thức bao quát và thời gian làm bài giới hạn, học sinh lớp 12 thường có xu hướng “lao” vào luyện đề mà quên đi nền tảng quan trọng nhất: lý thuyết ôn thi Toán tốt nghiệp THPT.

Việc nắm chắc lý thuyết ôn thi Toán tốt nghiệp THPT còn giúp học sinh rút ngắn thời gian xử lý những câu vận dụng cao. Trong đề thi, có rất nhiều bài toán mà bản chất là “giả nâng cao” nhưng nếu biết cách phân tích bằng lý thuyết thì lại có lời giải cực kỳ ngắn gọn. Đó chính là lý do nhiều học sinh điểm cao chia sẻ rằng: “Không phải luyện thật nhiều đề, mà là phải hiểu thật sâu lý thuyết”.

Với mục tiêu đó, bài viết này sẽ đi sâu vào những phần lý thuyết thường gặp và dễ mất điểm nhất trong đề thi Toán THPT: Tính đơn điệu, cực trị, giá trị lớn nhất – nhỏ nhất của hàm số, tiệm cận, và vectơ trong không gian. Đây là những phần vừa cơ bản, vừa có tính ứng dụng cao, giúp học sinh tự tin hơn trong giai đoạn nước rút.

1. Tính đơn điệu của hàm số

Khái niệm tính đơn điệu của hàm số
Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và y = f(x) là hàm số xác định trên K

Chú ý:

– Nếu hàm số đồng biến trên K thì đồ thị của hàm số đị lên từ trái sang phải (H.a).
– Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (H.b).

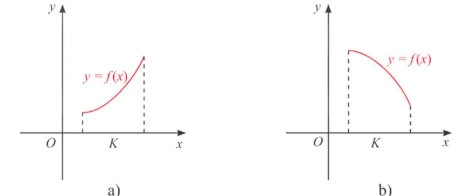
– Hàm số đồng biến hay nghịch biến trên K còn được gọi chung là đơn điệu trên K . Việc tìm các khoảng đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của hàm số.
– Khi xét tính đơn điệu của hàm số mà không chỉ rõ tập K thì ta hiểu là xét trên tập xác định của hàm số đó.

Định lý
Cho hàm số y = f(x) có đạo hàm trên khoảng K

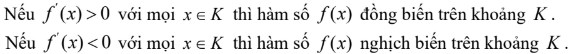
Chú ý:

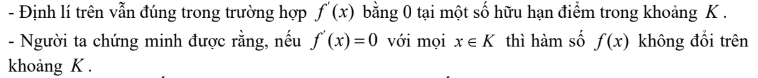
Sử dụng bảng biến thiên xét tính đơn đlệu của hàm số
Các bước để xét tính đơn điệu của hàm số y = f(x):

• Tìm tập xác định của hàm số.
• Tính đạo hàm f ‘(x). Tìm các điểm mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
• Sắp xếp các điểm i x theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
• Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Ví dụ 1: Xét tính đồng biến và nghịch biến của hàm số sau y=x³ – 6x² + 9x -3

Hướng dẫn

Tập xác định: D = R

Ta có y’ = 3x² – 12x + 9

y’ = 0 ⇔ 

Bảng biến thiên:

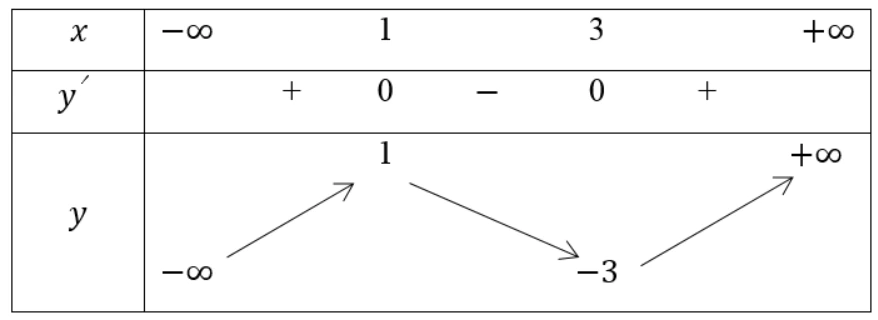
Vậy hàm số đồng biến trên các khoảng (-∞;1) và (3;+∞)

Hàm số nghịch biến trên khoảng (1;3)

Nắm vững tính đơn điệu của hàm số không chỉ là yêu cầu bắt buộc trong chương trình lớp 12 mà còn là phần kiến thức then chốt trong lý thuyết ôn thi Toán tốt nghiệp THPT. Việc thành thạo kỹ năng xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến sẽ giúp học sinh tự tin vượt qua các câu hỏi từ cơ bản đến nâng cao.

2. Cực trị của hàm số

Trong hệ thống lý thuyết ôn thi Toán tốt nghiệp THPT, cực trị đóng vai trò như “nút giao kiến thức” giữa khảo sát hàm số và ứng dụng giải bài toán thực tiễn. Đặc biệt, nhiều bài toán yêu cầu nhận diện cực trị dựa vào dấu đạo hàm – nếu không nắm lý thuyết rõ ràng, học sinh rất dễ chọn sai phương án dù chỉ sai một bước nhỏ.

Khái niệm cực trị của hàm số
Tổng quát, ta có định nghĩa sau:
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b)  a b ( a có thể là -∞,b có thể là +∞ ) và điểm

• Nếu tồn tại số h > 0 sao cho với mọi thì ta nói hàm số f (x) đạt cực đại tại
• Nếu tồn tại số h > 0 sao cho với mọi thì ta nói hàm số f (x) đạt cực tiểu tại.

Chú ý

• Nếu hàm số y = f(x) đạt cực đại tại thì được gọi là điểm cực đại của hàm số f (x) . Khi đó,  được gọi là giá trị cực đại của hàm số f(x) và kí hiệu là hay . Điểm được gọi là điểm cực đại của đồ thị hàm số.
• Nếu hàm số y = f(x) đạt cực tiểu tại thì được gọi là điểm cực tiểu của hàm số f(x) . Khi đó, được gọi là giá trị cực tiểu của hàm số f(x) và kí hiệu là hay . Điểm  được gọi là điểm cực tiểu của đồ thị hàm số.
• Các điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị) của hàm số.

Cách tìm cực trị của hàm số
ĐỊNH LÍ 1
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm và có đạo hàm trên các khoảng

a) Nếu với mọi là một điểm cực đại của hàm sốf(x) .
b) Nếu với mọi là một điểm cực tiểu của hàm sốf(x) .
Định lí trên được viết gọn lại trong hai bảng biến thiên sau:

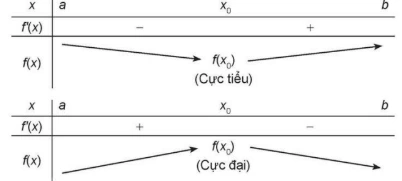
Chú ý.
Từ định lí trên ta có các bước tìm cực trị của hàm số y = f(x) như sau:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm . Tìm các điểm mà tại đó đạo hàm = 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Nếu không phải là điểm cực trị của hàm số. Chẳng hạn, hàm số nhưng x = 0 không phải là điểm cực trị của hàm số.

ĐỊNH LÍ 2.
Giả sử hàm số y = f(x) có đạo hàm cấp một trên (a; b) chứa điểm , có đạo hàm cấp hai khác 0 tại điểm

• Nếu thì hàm số y = f(x) đạt cực đại tại điểm
• Nếu 0 y x ”( ) 0  thì hàm số y = f(x) đạt cực tiểu tại điểm

Dạng 1. Tìm các điểm cực trị của hàm số.

1. Phương pháp giải.

Quy tắc 1: Áp dụng định lý 2

– Tìm  f’(x)

– Tìm các điểm x_i (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm

– Xét dấu của  f’(x). Nếu  f’(x) đổi dấu khi x qua điểm x_o  thì hàm số có cực trị tại điểm x_o

Quy tắc 2: Áp dụng định lý 3

– Tìm  f’(x)

– Tìm các nghiệm x_i (i = 1, 2, 3,…) của phương trình f ‘(x) = 0 

– Với mỗi x_i tính f ”(x_i)

– Nếu f ”(x_i) < 0 thì hàm số đạt cực đại tại điểm x_i

– Nếu f ”(x_i) > 0 thì hàm số đạt cực tiểu tại điểm x_i

Phần kiến thức này không phức tạp, nhưng đòi hỏi sự hiểu đúng và thao tác cẩn thận. Vì vậy, hãy đưa cực trị vào nhóm ưu tiên trong sổ tay lý thuyết ôn thi Toán tốt nghiệp THPT của mình, bởi chỉ cần vững vàng phần này, bạn đã có thể nắm chắc 0,5 đến 1 điểm quý giá trong tay.

3. Giá trị lớn nhất và nhỏ nhất của hàm số

Khi đã xác định được cực trị, học sinh lớp 12 cần bước tiếp đến một dạng toán cực kỳ quen mặt trong đề thi – đó là tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Dạng bài này không chỉ xuất hiện trong phần hàm số mà còn là nội dung cốt lõi của nhiều câu thực tiễn, đặc biệt là những bài liên quan đến hình học và ứng dụng.

ĐỊNH NGHĨA
Cho hàm số y = f(x) xác định trên tập D .

• Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu và tồn tại
  Kí hiệu

•  Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu và tồn tại
  Kí hiệu

Chú ý

• Ta quy ước rằng khi nói giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x( ) (mà không nói “trên tập D “) thì ta hiểu đó là giá trị lớn nhất hay giá trị nhỏ nhất của f x( ) trên tập xác định của hàm số.
• Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập D , ta thường lập bảng biến thiên của hàm số trên tập D để kết luận.

Cách tìm giá trị lớn nhất và giá trị nhỏ nhất trên miền D

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

$y = f(x)$

y=f(x) trên tập D xác định ta sẽ khảo sát sự biến thiên của hàm số trên D, rồi dựa vào kết quả bảng biến thiên của hàm số để đưa ra kết luận cho giá trị lớn nhất và nhỏ nhất.

Ví dụ 1: Giá trị lớn nhất, nhỏ nhất của hàm số là bao nhiêu?

$$y=x^3-3x^2-9x+5$$

Bảng biến thiên:

$$y = x^3 – 3x^2 – 9x + 5$$

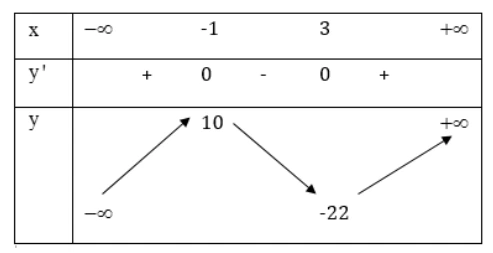
Vậy hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.

Ví dụ 2: Toán 12 tìm trị nhỏ nhất, lớn nhất của hàm số:

$$y=\frac{x^2+2x+3}{x-\mathrm{1<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">\; </span>}}$$

Phương pháp giải:

Như vậy, trong các bài toán tìm GTLN – GTNN trên một đoạn, học sinh chỉ cần nhớ công thức “3 điểm vàng”: tính giá trị tại hai đầu mút và tại các điểm nghi ngờ cực trị bên trong đoạn. Sau đó, so sánh để kết luận. Tuy đơn giản, nhưng nếu quên điều kiện xác định hoặc chọn sai miền, bài toán sẽ rơi vào bẫy sai lầm đáng tiếc.

4. Tiệm cận

Một trong những phần kiến thức mà nhiều học sinh lớp 12 thường bỏ sót hoặc học qua loa, chính là tiệm cận của hàm số. Tuy chiếm dung lượng không lớn trong đề thi, nhưng câu hỏi về tiệm cận thường xuất hiện dưới dạng trắc nghiệm nhận biết hoặc thông hiểu – rất dễ ghi điểm nếu nắm chắc lý thuyết. Trong hệ thống lý thuyết ôn thi Toán tốt nghiệp THPT, phần này đóng vai trò hỗ trợ cực kỳ quan trọng cho bài toán khảo sát và vẽ đồ thị hàm số, đặc biệt là các hàm phân thức bậc nhất, bậc hai.

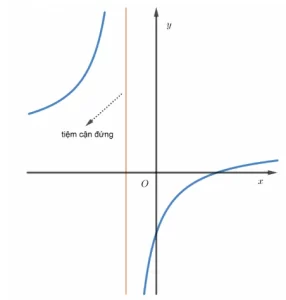
4.1. Tiệm cận đứng

Đường tiệm cận của một đồ thị hàm số

$y = f(x)$

y=f(x) được xác định bằng cách ta dựa vào tập xác định D để biết số giới hạn phải tìm.

Tiệm cận đứng của đồ thị hàm số

$y = f(x)$

là đường thẳng

$x = x_0$

​ nếu có ít nhất một trong các điều kiện sau thỏa mãn:

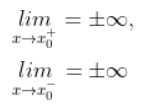
Cách tìm tiệm cận đứng đồ thị hàm số

Tiệm cận đứng của đồ thị hàm số được thực hiện theo các bước như sau:

• Bước 1: Xác định tập xác định D của hàm số.

• Bước 2: Xác định điểm hàm số không xác định nhưng có lân cận trái hoặc lân cận phải của điểm đó nằm bên trong tập xác định.

• Bước 3: Tính giới hạn một bên của hàm số tại các điểm được xác định ở bước 2 và kết luận.

Ví dụ: Cho hàm số

$y = \frac{x – 2}{x^2 – 4}$

Tiệm cận đứng của hàm số là?

Giải:

Tập xác định:

$$D = \mathbb{R} \setminus \{\pm 2\}$$

D=R∖{±2}

Ta có:

$$\lim_{x \to 2} f(x) = \lim_{x \to 2} \frac{x – 2}{x^2 – 4} = \lim_{x \to 2} \frac{1}{x – 2} = \frac{1}{0} \Rightarrow \text{không xác định}$$

→

$x = 2$

không là tiệm cận đứng vì giới hạn không tiến đến vô cực.

Xét:

$$\lim_{x \to -2^-} f(x) = \frac{x – 2}{x^2 – 4} = -\infty$$

$$\underset{x\to -2^{+}}{\lim }f(x)=\frac{x-2}{x^2-4}=+\mathrm{\infty }$$

⇒ x=−2 là tiệm cận đứng.

Kết luận: x=−2 là tiệm cận đứng của đồ thị hàm số.

Công thức tính nhanh tiệm cận đứng của đồ thị hàm số phân tuyến tính

Tiệm cận đứng của đồ thị phân tuyến tính

$y = \frac{ax + b}{cx + d}$ $(ad – bc \ne 0, c \ne 0)$

được tính nhanh bằng công thức:

Hàm số phân tuyến tính có một tiệm cận đứng duy nhất là:

$$x=-\frac{d}{c}$$

Ví dụ: Cho hàm số

$y = f(x) = \frac{x – 2}{x + 3}$

Tìm tiệm cận đứng theo công thức tính nhanh.

Giải:

Hàm số

$y = f(x) = \frac{x – 2}{x + 3}$

  có một đường tiệm cận đứng là:

$$x=-\frac{d}{c}=-3$$

Một số bài tập tìm đường tiệm cận đứng của đồ thị hàm số

Dạng 1: Xác định đường tiệm cận đứng dựa vào định nghĩa

Ta có: Tiệm cận đứng đồ thị hàm sốy=f(x) sẽ là đường thẳng

$x = x_0$

nếu thỏa mãn các điều kiện:

$$\lim_{x \to x_0^+} f(x) = \pm \infty, \quad \lim_{x \to x_0^-} f(x) = \pm \infty$$

Ví dụ: Cho đồ thị hàm số sau, hãy tìm tiệm cận đứng của hàm số:

• $y=\frac{2x-3}{x-\mathrm{1<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;\; font-size:\; 16px;"></span>}}$

Tập xác định:

$$D = \mathbb{R} \setminus \{1\}$$

$$\lim_{x \to 1^+} \frac{2x – 3}{x – 1} = -\infty, \quad \lim_{x \to 1^-} \frac{2x – 3}{x – 1} = +\infty$$

→ Vậy x=1 là tiệm cận đứng.

• $y = \frac{x^2 – 3x}{x^2 – 9}$​

$$\lim_{x \to 3^+} \frac{x^2 – 3x}{x^2 – 9} = \lim_{x \to 3^+} \frac{x(x – 3)}{(x – 3)(x + 3)} = \lim_{x \to 3^+} \frac{x}{x + 3} = \frac{3}{6} = \frac{1}{2}$$

$$\lim_{x \to -3^+} \frac{x^2 – 3x}{x^2 – 9} = \lim_{x \to -3^+} \frac{x(x – 3)}{(x – 3)(x + 3)} = \frac{-3}{0} \quad \text{(Không tiến đến vô cực)}$$

Kết luận: Vậy đồ thị hàm số

$y=f(x<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">)không\; có\; tiệm\; cận\; đứng.</span>$

Dạng 2: Tiệm cận đứng của đồ thị hàm số phân thức

$$y = \frac{ax + b}{cx + d} \quad \text{với} \quad (ad – bc \ne 0, \, c \ne 0)$$

⇒ Tiệm cận đứng:

$$x = -\frac{d}{c}$$

Ví dụ: Cho đồ thị hàm số, hãy tìm tiệm cận đứng của đồ thị đó:

$$y = f(x) = \frac{1 – 3x}{x + 2}$$

$$\lim_{x \to (-2)^+} \frac{1 – 3x}{x + 2} = +\infty$$

$$\lim_{x \to (-2)^-} \frac{1 – 3x}{x + 2} = -\infty$$

Kết luận:

$x = -2$

là tiệm cận đứng.

Dạng 3: Tìm tham số m để hàm số có tiệm cận đứng

Ví dụ 1: Giá trị của tham số

$m$

 là bao nhiêu để đồ thị hàm số

$$y=\frac{3x+1}{m-2x}$$

nhận đường thẳng x = 1 

$\mathrm{<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">là\; tiệm\; cận\; đứng?</span>}$

Giải:

Nghiệm của tử số

$= \frac{-1}{3}$

=3−1​

Để đồ thị hàm số có tiệm cận thì

$x = \frac{-1}{3}$

x=3−1​ không là nghiệm của phương trình

$m – 2x = 0$

m−2x=0 hay

$$m-2\left(\frac{-1}{3}\right)\mathrm{\ne }0\Rightarrow m\mathrm{\ne }\frac{-2}{3}$$

→ Đồ thị hàm số có

$x = \frac{m}{2}$

  là tiệm cận đứng

Để đồ thị hàm số nhận x=1 làm tiệm cận đứng thì:

$$\frac{m}{2}=1\Rightarrow m=2$$

Vậy giá trị tham số là m=2

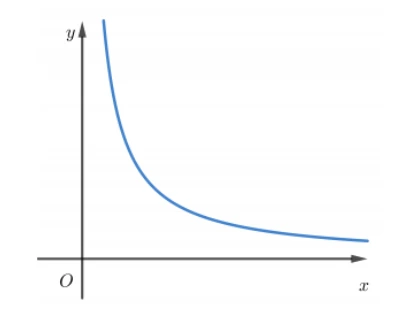
4.2. Tiệm cận ngang

Tiệm cận ngang của một đồ thị hàm sốy=f(x) xác định trên (a;+∞) là:

• Nếu limx→+∞​f(x)=b thì y=b là đường tiệm cận ngang của đồ thị hàm sốy=f(x).

• Nếu limx→−∞​f(x)=b thì y=b là đường tiệm cận ngang của đồ thị hàm sốy=f(x) xác định trên (−∞;a).

Vậy hàm số sẽ có tối đa 2 đường tiệm cận ngang và có thể không có đường tiệm cận ngang nào.

Cách tìm tiệm cận ngang của một đồ thị hàm số

Để tìm tiệm cận ngang của đồ thị hàm số y=f(x), ta làm theo các bước sau:

• Bước 1: Tìm tập xác định của hàm số.

• Bước 2: Tiếp theo, tính giới hạn của hàm số đó tại vô cực. Từ đó, đồ thị có chăng là các đường tiệm cận ngang.

Giả sử hàm sốy=f(x) có tập xác định là D.
Nếu

$\lim_{x \to -\infty} f(x) = y_0$

limx→−∞​f(x)=y0​ và limx→+∞​f(x)=y0​, thì đường thẳng y=y0​ là đường tiệm cận ngang của đồ thị hàm số.

Ví dụ: Cho hàm số

$y = \frac{x+1}{x+1}$

. Hãy tìm tiệm cận ngang của đồ thị hàm số đó.

Giải:
Tập xác định:

$D = \mathbb{R}$

Ta có:

$$\underset{x\to +\mathrm{\infty }}{\lim }\frac{x+1}{x+1}=1,\underset{x\to -\mathrm{\infty }}{\lim }\frac{x+1}{x+1}=1$$

→ Vậy đồ thị hàm số có một tiệm cận ngang là y

$y = 1$

Công thức tính tiệm cận ngang

Tiệm cận ngang của hàm phân thức hữu tỉ

Để tìm tiệm cận ngang của một hàm phân thức hữu tỉ, ta có công thức như bảng sau:

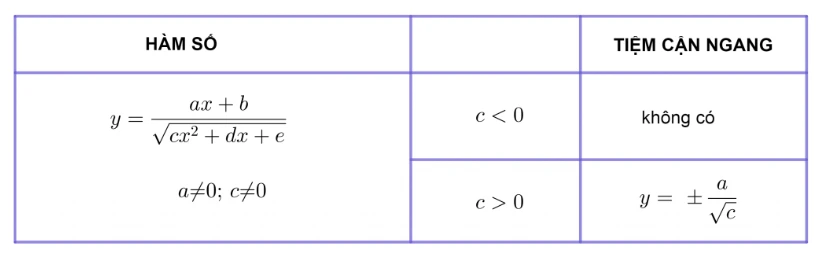
Tiệm cận ngang của hàm phân thức vô tỉ

Ta có công thức tính tiệm cận ngang của hàm phân thức vô tỉ là:

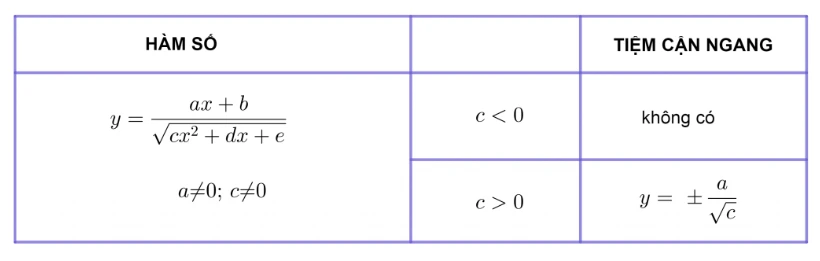
Một số bài tập tìm đường tiệm cận ngang của đồ thị hàm số

Bài 1: Cho đồ thị hàm số

$y = \frac{x + \sqrt{4x^2 – 3}}{2x + 3}$

tìm đường tiệm cận ngang của hàm số.

Giải:

$$\lim_{x \to -\infty} y = \frac{x + \sqrt{4x^2 – 3}}{2x + 3} = \frac{-1}{2}$$

$$\lim_{x \to +\infty} y = \frac{x + \sqrt{4x^2 – 3}}{2x + 3} = \frac{3}{2}$$

Kết luận:

$y = \frac{3}{2}$

và

$y = -\frac{1}{2}$

là tiệm cận ngang của đồ thị hàm số.

Bài 2: Tiệm cận ngang của đồ thị hàm số đã cho

$y = \frac{x – 1}{\sqrt{x^2 – 3x + 2}}$

là bao nhiêu?

Giải:

$$\lim_{x \to -\infty} y = \frac{1 – \frac{1}{x}}{\sqrt{1 – \frac{3}{x} + \frac{2}{x^2}}} = -1$$

$$\underset{x\to +\mathrm{\infty }}{\lim }y=\frac{1-\frac{1}{x}}{\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}}=1$$

Kết luận:

$y = 1$

và

$y=-\mathrm{1<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">là\; đường\; tiệm\; cận\; ngang\; của\; đồ\; thị\; hàm\; số.</span>}$

Hãy đưa nội dung tiệm cận vào nhóm “kiến thức chắc chắn phải làm đúng” trong lý thuyết ôn thi Toán tốt nghiệp THPT, bởi chỉ cần nắm vững quy tắc giới hạn và biết nhận diện đúng dạng hàm, bạn sẽ có thể xử lý dạng bài này một cách nhanh chóng và chính xác. Mỗi điểm nhỏ đều quý giá, và tiệm cận chính là một “điểm cộng dễ lấy” mà bạn không nên bỏ lỡ trong hành trình về đích kỳ thi tốt nghiệp.

Tổng kết

Nắm vững lý thuyết ôn thi Toán tốt nghiệp THPT không chỉ giúp học sinh tự tin xử lý các câu hỏi nhận biết và thông hiểu, mà còn tạo nền tảng vững chắc để giải nhanh các dạng toán vận dụng. Trong bối cảnh thời gian ôn thi gấp rút, việc hệ thống lại lý thuyết theo chuyên đề như hàm số, tiệm cận, vectơ… sẽ giúp tiết kiệm thời gian, tăng hiệu quả học tập, và đặc biệt phù hợp với định hướng ra đề hiện nay.

Để bổ sung kiến thức toàn diện, học sinh có thể tham khảo thêm Bộ sách ôn thi tốt nghiệp THPT – tài liệu chính thống và cập nhật theo cấu trúc đề thi mới nhất từ Bộ GD&ĐT. Đồng thời, đừng quên theo dõi các bài viết học tập hữu ích khác tại HEID – đơn vị  đồng hành cùng giáo viên và học sinh trong hành trình chinh phục kỳ thi quan trọng nhất bậc phổ thông.