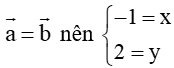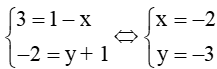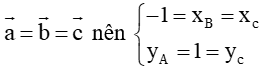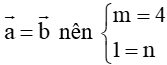Để vượt qua kỳ thi tuyển sinh vào lớp 10 một cách tự tin, việc nắm vững công thức toán ôn thi vào 10 là điều không thể thiếu. Trong đề thi Toán vào 10, phần hình học và đại số đều đòi hỏi học sinh phải vận dụng nhanh, chính xác các công thức đã học. Nếu không ghi nhớ tốt, việc giải bài toán trở nên khó khăn, thậm chí dễ mắc lỗi sai dù hiểu rõ bản chất. Ngược lại, khi học sinh có trong tay tuyển tập công thức toán ôn thi vào 10 được hệ thống một cách khoa học, rõ ràng và dễ nhớ, thì việc xử lý bài tập trở nên trơn tru hơn rất nhiều.

Trong nội dung dưới đây, bạn sẽ được cung cấp tổng hợp đầy đủ các công thức toán ôn thi vào 10 liên quan đến tọa độ điểm, vectơ, phép toán vectơ, trung điểm và trọng tâm tam giác – những dạng bài quen thuộc và có khả năng xuất hiện cao trong đề thi. Mỗi công thức đều được trình bày dễ hiểu, có ví dụ minh họa cụ thể để học sinh dễ hình dung và ghi nhớ.

Hãy cùng bắt đầu chinh phục kỳ thi vào 10 bằng cách xây dựng nền tảng thật vững chắc với những công thức toán ôn thi vào 10 không thể bỏ qua!

1/ Công thức xác định tọa độ của một vectơ, một điểm

Một trong những nền tảng quan trọng giúp học sinh giải tốt dạng bài này chính là hiểu và vận dụng đúng công thức toán ôn thi vào 10 liên quan đến tọa độ điểm và vectơ. Việc xác định tọa độ không chỉ giúp biểu diễn hình học chính xác trên mặt phẳng tọa độ, mà còn là bước khởi đầu cho nhiều phép biến đổi sau đó như: tính trung điểm, trọng tâm, chứng minh song song, thẳng hàng, vuông góc,…

Trong mặt phẳng tọa độ Oxy, với các vectơ đơn vị

$\overrightarrow{i}$

,

$\overrightarrow{j}$

tương ứng của các trục Ox và Oy.

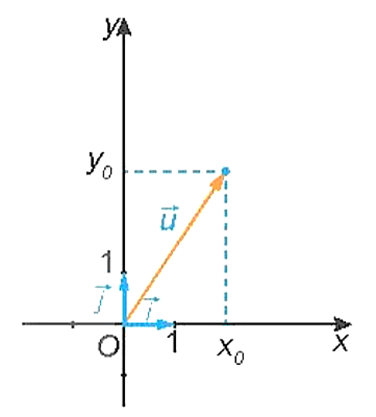Vectơ $\overrightarrow{u}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$, khi đó tọa độ vectơ $\stackrel{}{}$ $\overrightarrow{u}=\left(x_0;y_0\right)$– Trong mặt phẳng tọa độ Oxy, tọa độ vectơ  $\overrightarrow{OM}$ được gọi là tọa độ điểm M. $M\left(x_0;y_0\right)\iff \overrightarrow{OM}=x_0\overrightarrow{i}+y_0\overrightarrow{j}$

Ví dụ 1. Trong mặt phẳng tọa độ Oxy, hãy xác định tọa độ của các vectơ sau:

a)

$\overrightarrow{u}=–3\overrightarrow{i}+4\overrightarrow{j}$

b)

$\overrightarrow{v}=\overrightarrow{i}+\overrightarrow{j}$

c)

$\overrightarrow{a}=–7\overrightarrow{j}$

Hướng dẫn giải:

a) Vì

$\overrightarrow{u}=–3\overrightarrow{i}+4\overrightarrow{j}$

nên vectơ

$\overrightarrow{u}$

có tọa độ là (–3; 4).

b) Vì

$\overrightarrow{v}=\overrightarrow{i}+\overrightarrow{j}$

nên vectơ

$\overrightarrow{v}$

có tọa độ là (1; 1).

c) Vì

$\overrightarrow{a}=–7\overrightarrow{j}$

nên vectơ

$\overrightarrow{a}$

có tọa độ là (0; –7).

Ví dụ 2. Trong mặt phẳng tọa độ Oxy hãy biểu diễn vectơ sau theo các vectơ đơn vị

$\overrightarrow{i}$

, 

$\overrightarrow{j}$

a) 

$\overrightarrow{a}=\left(–1;–9\right)$

b) 

$\overrightarrow{b}=\left(–3;0\right)$

c) 

$\overrightarrow{c}=\left(5;–2\right)$

Hướng dẫn giải:

a) Vì

$\overrightarrow{a}=\left(–1;–\mathrm{9\; n}\right)$

ên

$\overrightarrow{a}=–\overrightarrow{i}–9\overrightarrow{j}$

b) Vì

$\overrightarrow{b}=\left(–3;0\right)$

nên

$\overrightarrow{b}=–3\overrightarrow{i}$

c) Vì

$\overrightarrow{c}=\left(5;–\mathrm{2 }\right)$

nên

$\overrightarrow{c}=5\overrightarrow{i}–2\overrightarrow{j}$

Việc nắm chắc công thức toán ôn thi vào 10 để xác định tọa độ điểm và tọa độ vectơ không chỉ giúp học sinh giải nhanh các bài hình học tọa độ, mà còn giúp làm chủ các bài toán có tính tư duy cao. Đây là một trong những kiến thức cơ bản nhưng đóng vai trò then chốt trong suốt quá trình ôn tập và làm bài thi. Hãy luyện tập thật nhiều để biến những công thức này thành phản xạ tự nhiên trong đầu bạn!

2/ Công thức Tọa độ hai vectơ bằng nhau

Khi ôn thi vào lớp 10, học sinh thường gặp các bài toán yêu cầu so sánh hai vectơ, chứng minh hai cạnh song song, bằng nhau hoặc kiểm tra xem ba điểm có thẳng hàng không. Đây đều là những dạng bài cơ bản nhưng dễ mất điểm nếu không nắm vững công thức. Trong số các công thức toán ôn thi vào 10, công thức xác định điều kiện để hai vectơ bằng nhau đóng vai trò cực kỳ quan trọng, giúp giải quyết nhanh gọn các dạng bài liên quan đến hình học phẳng.

Công thức

Trong mặt phẳng tọa độ Oxy cho 

$\overrightarrow{\mathrm{u(}}\left(x;\mathrm{y) }\right)$

và 

$\overrightarrow{v}\left(\mathrm{(x}‘;y‘)\right)$

Khi đó .

→ Hai vectơ bằng nhau khi và chỉ khi chúng có cùng tọa độ.

2. Ví dụ minh họa

Ví dụ 1.

a) Cho vectơ

$\overrightarrow{a}=\left(–1;2\right)$

. Tìm vectơ

$\overrightarrow{b}\left(x;y\right)$

, biết

$\overrightarrow{a}=\overrightarrow{b}$

.

b) Cho hình bình hành ABCD. Biết

$\overrightarrow{AB}\left(\mathrm{}\right)$

$(3;-2),$

$\overrightarrow{\mathrm{ D}C}\left(\mathrm{}\right)$

$\mathrm{(1}-x;y+1)$. Tìm giá trị x và y.

c) Cho

$\overrightarrow{a}=\overrightarrow{b}=\overrightarrow{c}$

. Tìm tọa độ vectơ

$\overrightarrow{c}$

, biết: 

$\overrightarrow{a}(–1;y_A),\overrightarrow{b}\left(x_B;1\right)$

Hướng dẫn giải:

a) Vì 

Vậy vectơ

$\overrightarrow{b}$

có tọa độ là (–1; 2).

b) Vì ABCD là hình bình hành nên

$\overrightarrow{AB}=\overrightarrow{DC}$

Suy ra 

Vậy x = –2 và y = –3.

c) Vì 

Vậy

$\overrightarrow{c}\left((-1;\mathrm{1)}\right)$

Ví dụ 2.

a) Cho vectơ

$\overrightarrow{a}=\left(m;1\right)$

,

$\overrightarrow{b}=\left(4;n\right)$

, biết

$\overrightarrow{a}=\overrightarrow{b}$

. Tính m + n.

b) Trên trục tọa độ (O;

$\overrightarrow{i}$

) cho điểm A có tọa độ là 7. Biết O

$\overrightarrow{A}=\overrightarrow{u}$

, tìm tọa độ vectơ 

$\overrightarrow{u}$

.

c) Trên trục tọa độ (O; 

$\overrightarrow{i}$

) cho điểm A có tọa độ là 2. Trên trục tọa độ (O; 

$\overrightarrow{j}$

) cho điểm B có tọa độ là 2. Hãy cho biết vectơ 

$\overrightarrow{OA},\overrightarrow{OB}$

có phải là hai vectơ bằng nhau không? Vì sao?

Hướng dẫn giải:

a) Vì 

Vậy m + n = 4 + 1 = 5.

b) Vì A thuộc trục tọa độ (O; 

$\overrightarrow{i}$

) nên A có tọa độ là (7; 0). Suy ra

$\overrightarrow{OA}=\left(7;0\right)$

Vì O

$\overrightarrow{A}=\overrightarrow{u}$

nên

$\overrightarrow{u}$ $(7;0)$

c) Vì A thuộc trục tọa độ (O; 

$\overrightarrow{i}$

) nên A có tọa độ là (2; 0). Suy ra

$\overrightarrow{OA}=\left(2;0\right)$

.

Vì B thuộc trục tọa độ (O; 

$\overrightarrow{j}$

) nên B có tọa độ là (0; 2).

Suy ra 

$\overrightarrow{OB}$

$=\left(0;2\right)$

Hai vectơ

$\overrightarrow{OA},\overrightarrow{OB}$

là hai vectơ không bằng nhau vì  .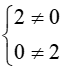

Nhờ có công thức toán ôn thi vào 10 liên quan đến tọa độ vectơ, học sinh có thể giải quyết bài toán một cách chính xác và ngắn gọn. Khi đã thành thạo kỹ năng này, bạn sẽ tiết kiệm rất nhiều thời gian trong phòng thi và dễ dàng đạt điểm tuyệt đối ở phần Hình học.

3/ Biểu thức tọa độ của các phép toán vectơ

Trong hành trình ôn thi vào lớp 10, việc hiểu rõ cách cộng, trừ, nhân vectơ sẽ giúp học sinh chủ động xử lý nhanh nhiều bài toán không gian phẳng. Vì vậy, các công thức toán ôn thi vào 10 về biểu thức tọa độ của phép toán vectơ chính là bộ công cụ không thể thiếu để bạn “lắp đúng mô hình – ra đúng kết quả”.

Công thức

a) Biểu thức tọa độ của các phép toán vectơ

Cho 

$\overrightarrow{u}(x;y)$

và 

$\overrightarrow{v}(x‘;y‘)$

, khi đó ta có:

• $\overrightarrow{u}+\overrightarrow{v}=(x+x‘;y+y‘)$ 

• $\overrightarrow{u}–\overrightarrow{v}=(x–x‘;y–y‘)$ 

• $k\overrightarrow{u}=\left(kx;ky\right)$ 

, với k ∈ ℝ.

b) Các tính chất:

– Tính chất của phép cộng vectơ:

• Tính chất giao hoán: $\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{v}+\overrightarrow{u}$ 
• Tính chất kết hợp: $(\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w}=\overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w})$ 
• Tính chất cộng với vectơ – không: $\overrightarrow{u}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{u}=\overrightarrow{u}$ 

– Tính chất của nhân vectơ với một số: Với hai vectơ

$\overrightarrow{u},\overrightarrow{v}$

và hai số thực k, t ta có:

• $\left(t\overrightarrow{u}\right)=\left(kt\right)\overrightarrow{u}$ 
• $(\overrightarrow{u}\pm \overrightarrow{v})=k\overrightarrow{u}\pm k\overrightarrow{v}$ 
• $(k+t)\overrightarrow{u}=k\overrightarrow{u}+t\overrightarrow{u}$ 
• $\overrightarrow{u}=\overrightarrow{u};(–1).\overrightarrow{u}=–\overrightarrow{u}$ 

Ví dụ 1. Cho các vectơ

$\overrightarrow{u}(1;–2)$

,

$\overrightarrow{v}(0;5)$

và

$\overrightarrow{w}(3;8)$

. Tìm tọa độ vectơ của các vectơ sau:

a)

$\overrightarrow{u}+\overrightarrow{v}$

b)

$\overrightarrow{u}–\overrightarrow{v}$

c)

$4\overrightarrow{w}$

Hướng dẫn giải:

a)

$\overrightarrow{u}+\overrightarrow{v}=(1+0;–2+5)=(1;3)$

b)

$\overrightarrow{u}–\overrightarrow{v}=(1–0;–2–5)=(1;–7)$

c)

$4\overrightarrow{w}=(4.3;4.8)=(12;32)$

Ví dụ 2. Cho

$\overrightarrow{u}(–4;–1)$

,

$\overrightarrow{v}(8;6)$

và

$\overrightarrow{w}(3;0)$

. Tìm tọa độ các vectơ sau:

a)

$2\overrightarrow{u}+\overrightarrow{v}$

b)

$\overrightarrow{u}–\overrightarrow{v}–\overrightarrow{w}$

c)

$\overrightarrow{u}+3\overrightarrow{v}–\overrightarrow{w}$

Hướng dẫn giải:

a) Ta có

$2\overrightarrow{u}=(–8;–2)$ $2\overrightarrow{u}+\overrightarrow{v}=(–8+8;–2+6)=(0;4)$

b) Ta có

$\overrightarrow{u}–\overrightarrow{v}=(–4–8;–1–6)=(–12;–7)$

Vậy

$\overrightarrow{u}–\overrightarrow{v}–\overrightarrow{w}=(–12–3;–7–0)=(–15;–7)$

c) Ta có .

Vậy .

Học vectơ không còn khô khan khi bạn biết cách biến mỗi công thức thành một thao tác trực quan, gắn với hình ảnh cụ thể. Trong số những công thức toán ôn thi vào 10 mà bạn cần nắm chắc, các phép toán vectơ là mắt xích quan trọng giúp bạn xử lý nhanh các bài hình học và tọa độ phức tạp. Hãy luyện tập thật nhiều để từ “lắp ghép đúng” chuyển thành “tư duy hình học đỉnh cao”!

4/ Liên hệ giữa tọa độ điểm và tọa độ của một vectơ trong mặt phẳng

Trong quá trình luyện đề, dạng toán này xuất hiện rất nhiều, và việc hiểu rõ công thức toán ôn thi vào 10 về mối liên hệ giữa điểm và vectơ chính là chìa khóa để bạn điều hướng chính xác trên “bản đồ toán học” này.

Công thức

– Cho hai điểm M(x; y) và N(x’; y’). Khi đó ta có:

$\overrightarrow{MN}=(x‘–x;y‘–y)$

– Quy tắc ba điểm: Với ba điểm O, M, N ta có:

$\overrightarrow{MN}=\overrightarrow{MO}+\overrightarrow{ON}=\overrightarrow{ON}–\overrightarrow{OM}$

Ví dụ 1. Cho hai điểm A(1; 3), B(0; 7) và C(–2; –2). Tìm tọa độ vectơ của các vectơ sau:

a) 

$\overrightarrow{AB}$

b) $2$

$\overrightarrow{AC}$

c)

$–\overrightarrow{BC}$

Hướng dẫn giải:

a) Ta có

$\overrightarrow{AB}=(0–1;7–3)=(–1;4)$

b) Ta có

$\overrightarrow{AC}=(–2–1;–2–3)=(–3;–5)$

Suy ra 

$2\overrightarrow{AC}=(–6;–10)$

c) Ta có

$\overrightarrow{BC}=(–2–0;–2–7)=(–2;–9)$

Suy ra

$\overrightarrow{BC}=$

(2;9)

Hiểu được mối liên hệ giữa điểm và vectơ giống như việc nắm rõ cách đọc bản đồ – xác định vị trí – tính toán hướng đi trong không gian hình học. Với những bạn đang ôn tập, đây là một phần kiến thức then chốt trong hệ thống công thức toán ôn thi vào 10 cần ghi nhớ. Khi thành thạo, bạn sẽ cảm thấy bài toán hình học không còn mơ hồ, mà trở thành những “bài tập dẫn đường” logic, rõ ràng và thú vị.

5/ Công thức tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác

Trong đề thi vào lớp 10, dạng bài liên quan đến trung điểm, trọng tâm thường dùng để chứng minh hình, dựng hình hoặc tìm tọa độ ẩn. Vì vậy, việc ghi nhớ chính xác công thức toán ôn thi vào 10 cho phần này sẽ giúp học sinh xử lý nhanh gọn các dạng bài quen thuộc nhưng dễ ăn điểm.

Công thức

Trong mặt phẳng tọa độ Oxy cho ba điểm A(x_A; y_A), B(x_B; y_B) và C(x_C; y_C) không thẳng hàng.

+ Tọa độ trung điểm M của đoạn thẳng AB là 

$\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right)$

+ Tọa độ trọng tâm G của tam giác ABC là

$\left(\frac{x_A+x_B+x_C}{3};\frac{y_A+y_B+y_C}{3}\right)$

– Chú ý:

+ Khi I là trung điểm của AB thì

$\overrightarrow{IA}+\overrightarrow{IB}=0$

+ Khi G là trọng tâm của tam giác ABC thì  

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0$

Ví dụ 1. Trong mặt phẳng tọa độ Oxy cho hai điểm A(–1; 0) và B(4; 7), C(–2; –5).

a) Tìm tọa độ trung điểm M của đoạn thẳng AB.

b) Tìm tọa độ trọng tâm G của tam giác ABC.

c) Tìm tọa độ trung điểm I của đoạn thẳng MG.

Hướng dẫn giải:

a) Tọa độ trung điểm M của đoạn thẳng AB là 

$\left(\frac{–1+4}{2};\frac{0+7}{2}\right)=\left(\frac{3}{2};\frac{7}{2}\right)$

b) Tọa độ trọng tâm G của tam giác ABC là 

$\left(\frac{–1+4–2}{3};\frac{0+7–5}{3}\right)=\left(\frac{1}{3};\frac{2}{3}\right)$

c) Tọa độ trung điểm I của đoạn thẳng MG là 

$\left(\frac{\frac{3}{2}+\frac{1}{3}}{2};\frac{\frac{7}{2}+\frac{2}{3}}{2}\right)=\left(\frac{11}{12};\frac{25}{12}\right)$

Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho ba điểmM(2; 0) và N(1; –3), P(0; 4) không thẳng hàng. Tìm tọa độ trung điểm H của đoạn thẳng MG, biết G là trọng tâm của tam giác MNP.

Hướng dẫn giải:

Tọa độ trọng tâm G của tam giác MNP là 

$\left(\frac{2+1+0}{3};\frac{0–3+4}{3}\right)=\left(1;\frac{1}{3}\right)$

Tọa độ trung điểm H của đoạn thẳng MG là 

$\left(\frac{2+1}{2};\frac{0+\frac{1}{3}}{2}\right)=\left(\frac{3}{2};\frac{1}{6}\right)$

Hiểu và áp dụng đúng công thức toán ôn thi vào 10 liên quan đến trung điểm và trọng tâm không chỉ giúp bạn giải nhanh các bài toán tọa độ mà còn thể hiện khả năng tư duy hình học sắc bén. Đây là phần kiến thức tưởng chừng cơ bản nhưng có thể giúp bạn ghi trọn điểm nếu luyện tập thành thạo.

Tổng kết

Việc nắm chắc công thức toán ôn thi vào 10 chính là bước khởi đầu vững vàng cho hành trình chinh phục kỳ thi chuyển cấp đầy thử thách. Từ những công thức xác định tọa độ điểm, tọa độ vectơ, đến trung điểm và trọng tâm tam giác – tất cả đều không chỉ là kiến thức cơ bản, mà còn là “vũ khí bí mật” giúp học sinh giải nhanh – đúng – chuẩn từng dạng bài trong đề thi.

Nếu bạn muốn luyện thêm nhiều đề thi chất lượng và được giải thích chi tiết bởi giáo viên giỏi, hãy tham khảo bộ sách Ôn thi vào lớp 10 môn Toán của Nhà xuất bản Giáo dục Việt Nam. Ngoài ra, đừng quên theo dõi thêm các bài viết phân tích chuyên sâu, mẹo làm bài và tài liệu ôn tập tại HEID – nơi cập nhật liên tục kiến thức từ SGK, đề thi và tài liệu bổ trợ cho học sinh THCS, THPT.

Chúc các bạn ôn tập thật tốt và đạt điểm cao trong kỳ thi vào 10 sắp tới!